题目内容
9.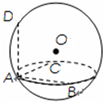 如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且AB=AC=$\sqrt{6}$,AD=2,则球O的体积为$\frac{32π}{3}$.
如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且AB=AC=$\sqrt{6}$,AD=2,则球O的体积为$\frac{32π}{3}$.
分析 由题意可得:球的半径R满足:(2R)2=$(\sqrt{6})^{2}+(\sqrt{6})^{2}+{2}^{2}$,解得R.即可得出.
解答 解:由A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且AB=AC=$\sqrt{6}$,AD=2,
则球的半径R满足:(2R)2=$(\sqrt{6})^{2}+(\sqrt{6})^{2}+{2}^{2}$,解得R=2.
∴球O的体积V=$\frac{4π}{3}×{2}^{3}$=$\frac{32π}{3}$.
故答案为:$\frac{32π}{3}$.
点评 本题考查了长方体的对角线与外接球的直径之间的关系、球的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
4.设函数f(x)=$\left\{\begin{array}{l}x^2,x≥0\\ ln(-x),x<0\end{array}$,则函数g(x)=f(x)-x的零点的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.对于任意的平面向量$\overrightarrow a$,$\overrightarrow b$,他们的夹角为θ,定义新运算$\overrightarrow a$?$\overrightarrow b$为向量$\overrightarrow a$在向量$\overrightarrow b$上的射影,即$\overrightarrow a$?$\overrightarrow b$=$\overrightarrow a$cosθ,若$\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$为平面向量,$\overrightarrow a$,$\overrightarrow c$的夹角为α,$\overrightarrow b$,$\overrightarrow c$的夹角为β,k∈R,则下列运算性质一定成立的是( )
| A. | $\overrightarrow a$?$\overrightarrow b$=$\overrightarrow b$?$\overrightarrow a$ | B. | (k$\overrightarrow a$)?$\overrightarrow b$=$\overrightarrow a$?(k$\overrightarrow b$) | C. | $\overrightarrow a$•($\overrightarrow b$?$\overrightarrow c$)=$\overrightarrow b$•($\overrightarrow a$?$\overrightarrow c$) | D. | |$\overrightarrow a$?$\overrightarrow b$|=$\frac{|\overrightarrow a•\overrightarrow b|}{\overrightarrow b}$ |
19.已知|${\overrightarrow a}$|=$\frac{1}{2}$|${\overrightarrow b}$|,函数f(x)=$\frac{1}{3}$x3+|${\overrightarrow a}$|x2+$\overrightarrow a$•$\overrightarrow b$x-|${\overrightarrow a$+$\overrightarrow b}$|在R上有极值,则向量$\overrightarrow a$与$\overrightarrow b$的夹角的范围是( )
| A. | [$0\;,\;\frac{π}{6}$) | B. | $(\frac{π}{6}\;,\;π)$ | C. | $(\frac{π}{3}\;,\;π)$ | D. | $(\frac{π}{3}\;,\;π$] |
 如图,两个椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1内部重叠区域的边界记为曲线C,P是曲线C上任意一点,给出下列三个判断:
如图,两个椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1内部重叠区域的边界记为曲线C,P是曲线C上任意一点,给出下列三个判断: