题目内容
8.已知抛物线C的顶点在平面直角坐标系原点,焦点在x轴上,若C经过点M(1,3),则其焦点到准线的距离为$\frac{9}{2}$.分析 由题意可知:设抛物线的方程:y2=2px,将M(1,3)代入9=2p,解得:p=$\frac{9}{2}$,求得抛物线方程,则焦点到准线的距离d=p=9.
解答 解:由题意可知:由焦点在x轴上,若C经过点M(1,3),
则图象经过第一象限,
∴设抛物线的方程:y2=2px,
将M(1,3)代入9=2p,解得:p=$\frac{9}{2}$,
∴抛物线的标准方程为:y2=9x,
由焦点到准线的距离d=p=$\frac{9}{2}$,
故答案为:$\frac{9}{2}$.
点评 本题考查抛物线的简单几何性质,考查抛物线方程的应用,属于基础题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
18.已知数列{an}的前n项和Sn=$\frac{n+1}{n+2}$,则a4=( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{30}$ | C. | 1 | D. | $\frac{7}{30}$ |
18.对于任意的平面向量$\overrightarrow a$,$\overrightarrow b$,他们的夹角为θ,定义新运算$\overrightarrow a$?$\overrightarrow b$为向量$\overrightarrow a$在向量$\overrightarrow b$上的射影,即$\overrightarrow a$?$\overrightarrow b$=$\overrightarrow a$cosθ,若$\overrightarrow a$,$\overrightarrow b$,$\overrightarrow c$为平面向量,$\overrightarrow a$,$\overrightarrow c$的夹角为α,$\overrightarrow b$,$\overrightarrow c$的夹角为β,k∈R,则下列运算性质一定成立的是( )
| A. | $\overrightarrow a$?$\overrightarrow b$=$\overrightarrow b$?$\overrightarrow a$ | B. | (k$\overrightarrow a$)?$\overrightarrow b$=$\overrightarrow a$?(k$\overrightarrow b$) | C. | $\overrightarrow a$•($\overrightarrow b$?$\overrightarrow c$)=$\overrightarrow b$•($\overrightarrow a$?$\overrightarrow c$) | D. | |$\overrightarrow a$?$\overrightarrow b$|=$\frac{|\overrightarrow a•\overrightarrow b|}{\overrightarrow b}$ |
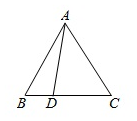 如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$.
如图,在△ABC中,若AB=AC=3,cos∠BAC=$\frac{1}{2}$,$\overrightarrow{DC}$=2$\overrightarrow{BD}$,则$\overrightarrow{AD}•\overrightarrow{BC}$=$-\frac{3}{2}$. 如图,两个椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1内部重叠区域的边界记为曲线C,P是曲线C上任意一点,给出下列三个判断:
如图,两个椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,$\frac{{y}^{2}}{25}$+$\frac{{x}^{2}}{9}$=1内部重叠区域的边界记为曲线C,P是曲线C上任意一点,给出下列三个判断: