题目内容
3.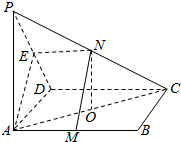 如图,己知P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,O是AC的中点.
如图,己知P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,O是AC的中点.(1)求证:MN∥平面PAD;
(2)若MN=BC=4,PA=4$\sqrt{3}$,求异面直线PA与MN所成的角的大小.
分析 (1)由已知推导出四边形AMNE是平行四边形,由此能证明MN∥平面PAD.
(2)连接MO,NO,推导出∠MNO就是PA与MN所成的角,由此能求出异面直线PA与MN所成的角的大小.
解答 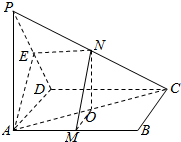 证明:(1)∵P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,
证明:(1)∵P是平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,E是PD的中点,
∴EN∥CD,EN=$\frac{1}{2}CD$,AM∥CD,AM=$\frac{1}{2}CD$,
∴EN$\underset{∥}{=}$AM,
∴四边形AMNE是平行四边形,
∴MN∥AE,
∵AE?平面PAD,MN?平面PAD,
∴MN∥平面PAD.
解:(2)连接MO,NO,
∵MN=BC=4,PA=4$\sqrt{3}$,∴MO=$\frac{1}{2}BC$=2,NO$\underset{∥}{=}$$\frac{1}{2}$PA=2$\sqrt{3}$,
∴∠MNO就是PA与MN所成的角,
在△MNO中,由余弦定理得cos∠MNO=$\frac{16+12-4}{2×4×2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
∴∠MNO=30°.
∴异面直线PA与MN所成的角的大小为30°.
点评 本题考查线面平行的证明,考查异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
13.函数f(x)=cosx的一个单调递增区间是( )
| A. | (0,$\frac{π}{2}$) | B. | (-$\frac{π}{2}$,$\frac{π}{2}$) | C. | (-π,0) | D. | (0,π) |
14.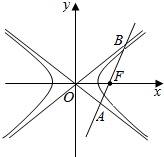 如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为11,12,经过右焦点F垂直于11的直线分别交11,12于A,B两点,若|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|依次成等差数列,则该双曲线的离心率为( )
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为11,12,经过右焦点F垂直于11的直线分别交11,12于A,B两点,若|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|依次成等差数列,则该双曲线的离心率为( )
 如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为11,12,经过右焦点F垂直于11的直线分别交11,12于A,B两点,若|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|依次成等差数列,则该双曲线的离心率为( )
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为11,12,经过右焦点F垂直于11的直线分别交11,12于A,B两点,若|$\overrightarrow{OA}$|,|$\overrightarrow{AB}$|,|$\overrightarrow{OB}$|依次成等差数列,则该双曲线的离心率为( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
15.下列全程命题中为真命题的是( )
| A. | 所有的质数都是奇数 | B. | ?x∈R,2x2+2≥2 | ||
| C. | 对每一个无理数x,x2也是无理数 | D. | 所有长度相等的向量均相等 |
13.假设要考查某企业生产的袋装牛奶的质量是否达标,现从500袋牛奶中抽取60袋进行检验,利用随机数表法抽取样本时,先将500袋牛奶按000,001,…,499进行编号,如果从随机数表第8行第26列的数开始,按三位数连续向右读取,最先检验的5袋牛奶的号码是(下面摘取了某随机数表第7行至第9行)( )
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211.
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211.
| A. | 455 068 047 447 176 | B. | 169 105 071 286 443 | ||
| C. | 050 358 074 439 332 | D. | 447 176 335 025 212 |
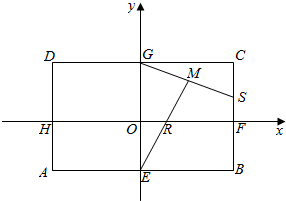 矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.
矩形ABCD中,|AB|=8,|BC|=6.E,F,G,H分别是矩形四条边的中点,R,S分别是线段OF和线段CF上的动点,且$\frac{OR}{OF}$=$\frac{CS}{CF}$=λ,建立如图所示的直角坐标系,O为矩形的对称中心,坐标轴分别平行于AB,BC.