题目内容
19.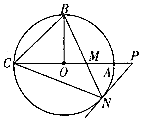 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于点N,过点N的切线交CA的延长线于点P,连接BC,CN.
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于点N,过点N的切线交CA的延长线于点P,连接BC,CN.(1)求证:∠BCN=∠PMN;
(2)若∠BCN=60°,PM=1,求OM的长.
分析 (1)连接ON,则ON⊥PN,由半径相等可得OB=ON,可得∠OBM=∠ONB,利用切线的性质和已知可得∠BOM=∠ONP=90°,进而可得∠PMN=∠PNM,再利用切割线定理即可证明;
(2)证明△PMN为等边三角形,得到MN=PM=1.设圆的半径为r,则在△BOM中,OB=r,OM=$\frac{r}{\sqrt{3}}$,MB=$\frac{2r}{\sqrt{3}}$,根据相交弦定理MB•MN=MA•MC,即可得出结论.
解答  (1)证明:连接ON,则ON⊥PN,∵OB=ON,∴∠OBM=∠ONB,
(1)证明:连接ON,则ON⊥PN,∵OB=ON,∴∠OBM=∠ONB,
∵PN是⊙O的切线,∴ON⊥NP.
∵BO⊥AC,
∴∠BOM=∠ONP=90°,∴∠OMB=∠MNP.
又∠BMO=∠PMO,∴∠PNM=∠PMN,
∵∠BCN=∠PNM,
∴∠BCN=∠PMN;
(2)解:∵∠PNM=∠PMN=∠BCN=60°,
∴△PMN为等边三角形,
∴MN=PM=1.
设圆的半径为r,则在△BOM中,OB=r,OM=$\frac{r}{\sqrt{3}}$,MB=$\frac{2r}{\sqrt{3}}$
根据相交弦定理MB•MN=MA•MC,
可得$\frac{2r}{\sqrt{3}}×1=(r-\frac{r}{\sqrt{3}})(r+\frac{r}{\sqrt{3}})$,∴r=$\sqrt{3}$,
∴OM=1.
点评 本题考查圆的切割线定理、相交弦定理的运用,考查推理和运算能力,属于中档题.

练习册系列答案
相关题目
10.若不等式-x+a+1≥0对一切x∈(0,$\frac{1}{2}$]成立,则a的最小值为( )
| A. | 0 | B. | -2 | C. | -$\frac{5}{2}$ | D. | -$\frac{1}{2}$ |
7.圆x2+y2+4x-2y+a=0截直线x+y+5=0所得弦的长度为2,则实数a=( )
| A. | -4 | B. | -2 | C. | 4 | D. | 2 |
4.《张丘建算经》中女子织布问题为:某女子善于织布,一天比一天织得快,且从第2天开始,每天比前一天多织相同量的布,已知第一天织5尺布,一月(按30天计)共织390尺布,则从第2天起每天比前一天多织( )尺布.
| A. | $\frac{1}{2}$ | B. | $\frac{8}{15}$ | C. | $\frac{16}{31}$ | D. | $\frac{16}{29}$ |
 如图所示,在四面体ABCD中,AD=1,CD=3,AC=2$\sqrt{3}$,cosB=$\frac{{\sqrt{3}}}{3}$.
如图所示,在四面体ABCD中,AD=1,CD=3,AC=2$\sqrt{3}$,cosB=$\frac{{\sqrt{3}}}{3}$.