题目内容
用辗转相除法求294和84的最大公约数时，需要做除法的次数是（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：用辗转相除计算最大公约数
专题：计算题,算法和程序框图
分析：用大数除以小数，得到商和余数，再用上面的除数除以余数，又得到商和余数，继续做下去，知道刚好能够整除为止，得到两个数的最大公约数，从而得到需要做除法的次数．
解答：
解：∵294÷84=3…42，
84÷42=2，
∴用辗转相除法求294和84的最大公约数时，需要做除法的次数2．
故选：B．
84÷42=2，
∴用辗转相除法求294和84的最大公约数时，需要做除法的次数2．
故选：B．
点评：本题考查辗转相除法，这是一个算法案例，还有一个求最大公约数的方法是更相减损法，这种题目出现的比较少，但是要掌握题目的解法．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
相关题目
执行如图的程序，若输入的实数x=4，则输出结果为（ ）| A、4 | ||
| B、3 | ||
| C、2 | ||
D、
|
为了得到函数y=cos（x-
）的图象，只需把函数y=cosx图象上所有的点（ ）
| 1 |
| 3 |
A、向左平行移动
| ||
B、向左平行移动
| ||
C、向右平行移动
| ||
D、向右平行移动
|
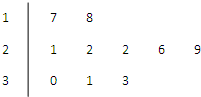如图是某公司10个销售店某月销售某产品数量（单位：台）的茎叶图，则数据落在区间[20，30）内的概率为（ ）| A、0.2 | B、0.4 |
| C、0.5 | D、0.6 |
在△ABC中，a=
b，A=2B，则cosB等于（ ）
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，将1，2，3，4，5，6，7，8，9共9个数填入该图中，其中1，4，9已经如图填好．要求每一行的数字从左到右递增，每一列的数字从上到下递增，每一个数字只能填一次，则共有（ ）种不同的填法．| A、12 | B、24 | C、30 | D、10 |
| ||
cos20°-
|
A、
| ||
B、
| ||
| C、1 | ||
| D、-1 |