题目内容
10.下列函数中,最小正周期为π且一条对称轴为$x=\frac{π}{8}$的函数是( )| A. | y=sin2x+cos2x | B. | y=sinx+cosx | C. | $y=cos(2x+\frac{π}{2})$ | D. | $y=sin(2x+\frac{π}{2})$ |
分析 依次化简各选项,求出最小正周期,和当$x=\frac{π}{8}$时函数是否取得最值.可得答案.
解答 解:对于A:y=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),最小正周期T=$\frac{2π}{2}=π$,当$x=\frac{π}{8}$时,y=$\sqrt{2}$,∴A对;
对于B:y=sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$),最小正周期T=2π,∴B不对;
对于C:y=cos(2x$+\frac{π}{2}$)=-sin2x,最小正周期T=$\frac{2π}{2}=π$,当$x=\frac{π}{8}$时,y=1,∴C不对.
对于C:y=sin(2x$+\frac{π}{2}$)=cos2x,最小正周期T=$\frac{2π}{2}=π$,当$x=\frac{π}{8}$时,y=1,∴D不对.
故选:A.
点评 本题主要考查三角函数的图象和性质的运用,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
15.极坐标为(1,π)的点M的直角坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (-1,0) | D. | (0,-1) |
2.某学校记者团由理科组和文科组构成,具体数据如表所示:
学校准备从中选4人到社区举行的大型公益活动中进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生,给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.
(Ⅰ)求理科组恰好记4分的概率;
(Ⅱ)设文科组男生被选出的人数为X,求随机变量的分布列X和数学期望E(x).
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 3 | 3 | 3 | 1 |
(Ⅰ)求理科组恰好记4分的概率;
(Ⅱ)设文科组男生被选出的人数为X,求随机变量的分布列X和数学期望E(x).
20.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,|$\overrightarrow{a}$|=1,|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{13}$,则|$\overrightarrow{b}$|=( )
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2$\sqrt{2}$ | D. | 2 |
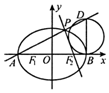 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,左、右焦点为F1,F2,点M为椭圆C上的任意一点,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值为2.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,左、右焦点为F1,F2,点M为椭圆C上的任意一点,$\overrightarrow{M{F_1}}•\overrightarrow{M{F_2}}$的最小值为2.