题目内容
1.已知函数f(x)=x3+ax2+bx-a2-7a在x=1处取的极大值为10,求a和b的值.分析 求出函数的导数,利用导函数为0,结合函数f(x)=x3+ax2+bx-a2-7a在x=1处取的极大值为10,求出a,b,然后验证即可.
解答 解:函数f(x)=x3+ax2+bx-a2-7a
可得:f′(x)=3x2+2ax+b,
∵x=1时,f(x)取得极值为10,
∴$\left\{\begin{array}{l}f'(1)=3+2a+b=0\\ f(1)=1+b-{a^2}-6a=10\end{array}\right.$,解得$\left\{\begin{array}{l}a=-2\\ b=1\end{array}\right.$或$\left\{\begin{array}{l}a=-6\\ b=9\end{array}\right.$
经检验$\left\{\begin{array}{l}a=-2\\ b=1\end{array}\right.$取得极小值舍去.
∴a=-6,b=9.
点评 本题考查函数的极值的求法,导函数的应用,注意验证,这是易错点.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
9.函数f(x)=log2x-$\frac{1}{2}$x+5的零点个数为( )
| A. | 0 | B. | 1 | C. | 3 | D. | 2 |
10.设x3+ax+b=0,其中a,b均为实数,给出下列条件中,①a=-3,b=-3;②a=-3,b=2;③a=0,b=2.其中能使得该三次方程仅有一个实根的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
10.已知函数f(x)=lnx-$\frac{m}{x}$(m∈R)在区间[1,e]上取得最小值4,则m=( )
| A. | -3e | B. | -1 | C. | -e3 | D. | e2 |
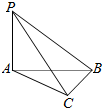 如图,Rt△ABC中,∠ACB=90°,∠BAC=45°,PA⊥平面ABC,且PA=BC=1,则二面角A-PB-C的平面角是60°.
如图,Rt△ABC中,∠ACB=90°,∠BAC=45°,PA⊥平面ABC,且PA=BC=1,则二面角A-PB-C的平面角是60°.