题目内容
10.已知抛物线C:x2=8y的焦点为F,动点Q在C上,圆Q的半径为1,过点F的直线与圆Q切于点 P,则$\overrightarrow{F{P}}•\overrightarrow{FQ}$的最小值为3.分析 可作出图形,由图形可看出$\overrightarrow{FP}•\overrightarrow{FQ}=|\overrightarrow{FQ}{|}^{2}-1$,而根据抛物线的定义,|FQ|等于Q到抛物线C的准线y=-2的距离,根据图形便可看出Q到准线的最短距离为2,从而便可得出$\overrightarrow{FP}•\overrightarrow{FQ}$的最小值为3.
解答 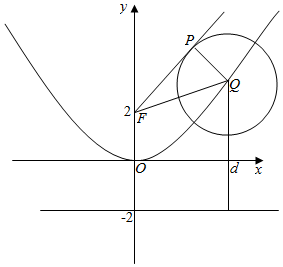 解:如图,$\overrightarrow{FP}•\overrightarrow{FQ}={|{\overrightarrow{FP}}|^2}={|{\overrightarrow{FQ}}|^2}-{r^2}={|{\overrightarrow{FQ}}|^2}-1$;
解:如图,$\overrightarrow{FP}•\overrightarrow{FQ}={|{\overrightarrow{FP}}|^2}={|{\overrightarrow{FQ}}|^2}-{r^2}={|{\overrightarrow{FQ}}|^2}-1$;
由抛物线的定义知:$|{\overrightarrow{FQ}}|=d,d$为点Q到准线的距离,易知,抛物线的顶点到准线的距离⑥最短,${|{\overrightarrow{FQ}}|_{min}}=2$;
∴${(\overrightarrow{FP}•\overrightarrow{FQ})_{min}}=3$;
即$\overrightarrow{FP}•\overrightarrow{FQ}$的最小值为3.
故答案为:3.
点评 考查圆心和切点连线垂直于切线,余弦函数的定义,直角三角形边的关系,以及抛物线的定义,抛物线的标准方程,抛物线的焦点和准线,以及数形结合解题的方法.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
20.已知F1,F2分别是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的左.右焦点,且|F1F2|=2,若P是该双曲线右支上的一点,且满足|PF1|=2|PF2|,则△PF1F2面积的最大值是( )
| A. | 2 | B. | $\frac{5}{3}$ | C. | $\frac{4}{3}$ | D. | 1 |
1.已知命题p:若a<1,则a2<1,下列说法正确的是( )
| A. | 命题p是真命题 | B. | 命题p的逆命题是真命题 | ||
| C. | 命题p的否命题是:若a<1,则a2≥1 | D. | 命题p的逆否命题是:若a2≥1,则a<1 |
18.已知复数w满足w-1=(1+w)i(i为虚数单位),则w=( )
| A. | 1-i | B. | -i | C. | -1+i | D. | i |
15.“a>1”是当“0<x≤2时,2-2x≥logax成立”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
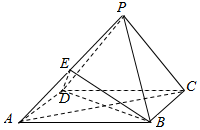 如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.
如图,在四棱锥P-ABCD中,底面为矩形,平面PCD丄平面ABCD,PC丄PD,PD=AD,E为PA的中点.