题目内容
19．已知Sn为等差数列{an}的前n项和，a1=4，a2+a3+a4=18，则使$\frac{{S}_{5}}{{S}_{n}}$∈Z的正整数n的值为（ ）| A． | 3 | B． | 4 | C． | 3或5 | D． | 4或5 |
分析 由题意可得a3=6，a2=5，由等差数列的求和公式和性质验证可得．
解答 解：∵a2+a3+a4=3a3=18，∴a3=6，
∴公差d=$\frac{1}{2}$（a3-a1）=1，故a2=5，
∴$\frac{{S}_{5}}{{S}_{3}}$=$\frac{5{a}_{3}}{3{a}_{2}}$=2∈Z，$\frac{{S}_{5}}{{S}_{5}}$=1∈Z，
当n=1、2、4、6、7、8…时，$\frac{{S}_{5}}{{S}_{n}}$∉Z
故选：C．
点评 本题考查等差数列的求和公式，涉及等差数列的性质，属基础题．
练习册系列答案
相关题目
14．
已知函数y=f（x）的图象是折线ABCDE，如图，其中A（1，2），B（2，1），C（3，2），D（4，1），E（5，2），若直线y=kx+b与y=f（x）的图象恰有四个不同的公共点，则k的取值范围是（ ）
已知函数y=f（x）的图象是折线ABCDE，如图，其中A（1，2），B（2，1），C（3，2），D（4，1），E（5，2），若直线y=kx+b与y=f（x）的图象恰有四个不同的公共点，则k的取值范围是（ ）| A． | （-1，0）∪（0，1） | B． | $（-\frac{1}{3}，\frac{1}{3}）$ | C． | （0，1] | D． | $[{0.\frac{1}{3}}]$ |
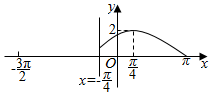已知定义在区间[-$\frac{3π}{2}$，π]上的函数y=f（x）的图象关于直线x=-$\frac{π}{4}$对称，当x∈[-$\frac{π}{4}$，π]时，函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$），且其图象如图所示．
9．若x＞1，y＞$\frac{1}{2}$，不等式$\frac{{x}^{2}}{a（2y-1）}$+$\frac{4{y}^{2}}{a（x-1）}$≥1恒成立，则实数a的最大值是（ ）
| A． | 8 | B． | 4 | C． | 2$\sqrt{2}$ | D． | $\sqrt{2}$ |