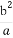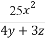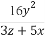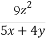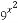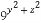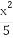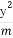题目内容
已知f(x)=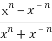 ,n∈N*,试比较f(
,n∈N*,试比较f(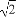 )与
)与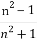 的大小,并且说明理由.
的大小,并且说明理由.
见解析
【解析】f(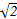 )=
)=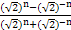 =
=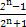
=1-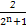 ,
,
而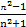 =1-
=1-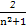 ,
,
∴f(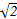 )与
)与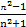 的大小等价于2n与n2的大小.
的大小等价于2n与n2的大小.
当n=1时,21>12;当n=2时,22=22;
当n=3时,23<32;当n=4时,24=42;
当n=5时,25>52.猜想当n≥5时,2n>n2.
以下用数学归纳法证明:
①当n=5时,由上可知不等式成立;
②假设n=k(k≥5,k∈N*)时,
不等式成立,即2k>k2,
则当n=k+1时,2k+1=2·2k>2k2,
又∵2k2-(k+1)2=(k-1)2-2>0(∵k≥5),即2k+1>(k+1)2,
∴n=k+1时,不等式成立.
综合①②对n≥5,n∈N*不等式2n>n2成立.
∴当n=1或n≥5时,f(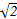 )>
)>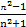 ;
;
当n=3时,f(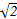 )<
)<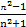 ;
;
当n=2或4时,f(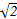 )=
)=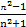 .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目