题目内容
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
(1)求证:AC⊥B1C;
(2)若D是AB中点,求证:AC1∥平面B1CD.
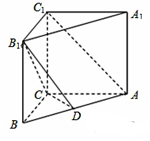
(1)要证明AC⊥B1C,根据线面垂直的判定定理,只要转化证明AC⊥平面BB1C1C即可;
(2)要证明AC1∥平面B1CD,根据线面的判定定理,只要转换证明DE//AC1即可.
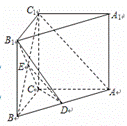 试题解析:(1)证明:在△ABC中,因为AB=5,AC=4,BC=3,
试题解析:(1)证明:在△ABC中,因为AB=5,AC=4,BC=3,
所以AC2+BC2=AB2,所以AC⊥BC.
因为直三棱柱ABC-A1B1C1,所以CC1⊥AC,
因为BC∩AC=C,所以AC⊥平面BB1C1C.
所以AC⊥B1C. 6分
(2)连结BC1,交B1C于E,连接DE.
因为直三棱柱ABC-A1B1C1,D是AB中点,所以侧面BB1C1C为矩形,
DE为△ABC1的中位线,所以DE//AC1.
因为DE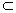 平面B1CD,AC1
平面B1CD,AC1 平面B1CD,所以AC1∥平面B1CD. 12分
平面B1CD,所以AC1∥平面B1CD. 12分
考点:空间位置关系的证明.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
(3)直线与平面垂直的性质
| 类别 | 语言表述 | 图示 | 字母表示 | 作用 |
| 性质 | (1)若一条直线与一个平面垂直,则这条直线垂直于平面内的__ 直线 |
|
| 证两条直线垂直 |
| (2)如果两条直线__________一个平面,那么这两条直线平行 |
|
| 证两条直线平行 |
 与平行四边形
与平行四边形 共边
共边 ,
, 、
、 分别在对角线
分别在对角线 、
、 上,且
上,且 . 求证:
. 求证: 平面
平面 .
.
 B.
B. C.
C. D.
D.






 ,C是弧AB的中点.
,C是弧AB的中点.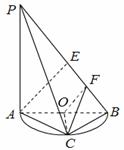 (1)证明:BC^平面PAC;
(1)证明:BC^平面PAC; 的正方形
的正方形 中,
中, 、
、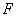 分别为
分别为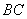 、
、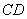 的中点,
的中点,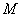 、
、 分别为
分别为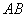 、
、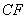 的中点,现沿
的中点,现沿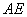 、
、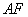 、
、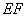 折叠,使
折叠,使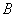 、
、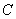 、
、 三点重合,构成一个三棱锥.
三点重合,构成一个三棱锥.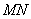 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明;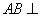 平面
平面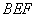 ;
; (3)求多面体
(3)求多面体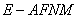 的体积.
的体积.
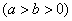 的离心率为
的离心率为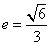 ,且椭圆C上的点到点
,且椭圆C上的点到点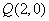 的距离的最大值为3.
的距离的最大值为3.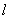 与椭圆C交于A、B两点,若在x轴上存在一点
与椭圆C交于A、B两点,若在x轴上存在一点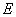 ,使
,使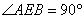 ,求直线
,求直线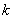 的取值范围.
的取值范围.