题目内容
设A、B是直线3x+4y+2=0与圆x2+y2+4y=0的两个交点，则线段AB的垂直平分线的方程是 ．
考点：直线与圆的位置关系
专题：直线与圆
分析：根根线段AB的垂直平分线过圆的圆心，且和直线AB垂直，求出圆心坐标和直线的斜率即可得到结论．
解答：
解：∵A、B是直线3x+4y+2=0与圆x2+y2+4y=0的两个交点，
∴线段AB的垂直平分线过圆的圆心，且和直线AB垂直，
则垂直平方线的斜率k=
，
圆的标准方程是x2+（y+2）2=4，
则圆心坐标为（0，-2），半径R=2，
则垂直平分线的方程为y+2=
x，
即4x-3y-6=0，
故答案为：4x-3y-6=0
∴线段AB的垂直平分线过圆的圆心，且和直线AB垂直，
则垂直平方线的斜率k=
| 4 |
| 3 |
圆的标准方程是x2+（y+2）2=4，
则圆心坐标为（0，-2），半径R=2，
则垂直平分线的方程为y+2=
| 4 |
| 3 |
即4x-3y-6=0，
故答案为：4x-3y-6=0
点评：本题主要考查直线和圆的位置关系的应用，利用AB垂直平分线的性质是解决本题的关键．
练习册系列答案
教学练新同步练习系列答案
相关题目
若复数z=（a2-4）+（a+2）i为纯虚数，则
的值为（ ）
| a+i2015 |
| 1+2i |
| A、1 | B、-1 | C、i | D、-i |
如图，在矩形ABCD中，AB=3，BC=6，点E为BC的中点，点F在CD边上，若
=2
，则
•
的值为（ ）
| DF |
| FC |
| AE |
| BF |
| A、-12 | B、12 |
| C、-15 | D、15 |
在18cm长的线段AB上任取一点M，并以线段AM为边作正方形，则点M使得此正方形面积介于25cm2到81cm2之间的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=2x和g（x）=x3的图象的示意图如图所示，设两函数的图象交于点A（x1，y1）B（x2，y2），且x1＜x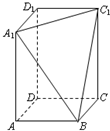
在长方体ABCD-A1B1C1D1中，AD=DC=