题目内容
如图,在长方体ABCD-A1B1C1D1中,A1A=AD=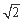 AB,E为线段A1D上一点.
AB,E为线段A1D上一点.
(Ⅰ)当E为A1D的中点时,求证:直线A1B∥平面EAC;
(Ⅱ)是否存在点E使二面角E-AC-D为30°?若存在,求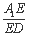 ,若不存在,说明理由.
,若不存在,说明理由.
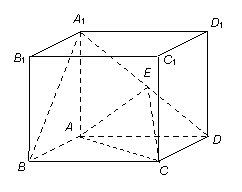
(Ⅰ)证明:设AC和BD交于点O,连EO,
由E,O分别是A1D,BD的中点,故EO∥A1B,…… 4分
∵EOÌ平面EAC,A1BË平面EAC,
 所以直线A1B∥平面EAC. …………………………… 6分
所以直线A1B∥平面EAC. …………………………… 6分
(Ⅱ) 过E作EG⊥AD于G,过G作GH⊥AC于H,连EH,
∴EG⊥底面ABCD,∴EG⊥AC,
∴AC⊥面EGH,∴EH⊥AC,
∴∠EHG为二面角E-AC-D的平面角.
设 ,则
,则 ,
,
∴ ,又
,又 ,∴
,∴ ,∴
,∴ ,
,
∴ ,∴
,∴ ,
,
所以存在点E满足条件,且 . …
. …


练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 中,
中,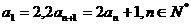 则
则 的值为
的值为  在点
在点 处的切线方程 .
处的切线方程 .
 若使z=ax+y取得最大值的最优解有无穷多个,则实数a的取值集合是( )
若使z=ax+y取得最大值的最优解有无穷多个,则实数a的取值集合是( )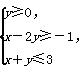 表示的平面区域内的任意一点,向量m=(1,1),n=(2,1),若
表示的平面区域内的任意一点,向量m=(1,1),n=(2,1),若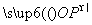 =λm+μn(λ,μ∈R),则μ的最大值为( )
=λm+μn(λ,μ∈R),则μ的最大值为( )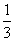 C.0 D.-1
C.0 D.-1 n展开式的二项式系数之和为32,常数项为80,则a的值为( )
n展开式的二项式系数之和为32,常数项为80,则a的值为( )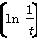 ≤2f(1),那么t的取值范围是________.
≤2f(1),那么t的取值范围是________.