题目内容
8．如果双曲线的方程是：$\frac{x^2}{9}-{y^2}=1$，则直线$y=\frac{1}{3}（x+1）$与此双曲线的交点个数为（ ）| A． | 1个 | B． | 0个 | C． | 2个 | D． | 无数个 |
分析 求得双曲线的渐近线方程，由直线$y=\frac{1}{3}（x+1）$与渐近线y=$\frac{1}{3}$x平行，且过点（-1，0），则直线$y=\frac{1}{3}（x+1）$与此双曲线仅有一个交点．
解答 解：双曲线的渐近线方程：y=±$\frac{1}{3}$x，焦点坐标为（±$\sqrt{10}$，0），
由直线$y=\frac{1}{3}（x+1）$与渐近线y=$\frac{1}{3}$x平行，且过点（-1，0），
点（-1，0）在双曲线内部，则直线$y=\frac{1}{3}（x+1）$与此双曲线仅有一个交点，
故选A．
点评 本题考查双曲线的渐近线方程的求法，考查直线与双曲线的交点的个数的求法，属于基础题．
练习册系列答案
相关题目
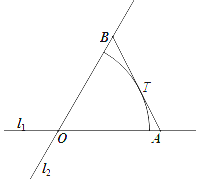如图，在某商业区周边有两条公路l1和l2，在点O处交汇；该商业区为圆心角$\frac{π}{3}$、半径3km的扇形．现规划在该商业区外修建一条公路AB，与l1，l2分别交于A，B，要求AB与扇形弧相切，切点T不在l1，l2上．
16．阅读下列程序：如果输入x=-2，则输出的结果y为（ ）
| A． | 0 | B． | -1 | C． | -2 | D． | 9 |
13．函数$y=\frac{x^2}{2^x}$的单调增区间是（ ）
| A． | $（0，\frac{2}{ln2}）$ | B． | $（-∞，0），（\frac{2}{ln2}，+∞）$ | C． | $（-∞，\frac{2}{ln2}）$ | D． | $（\frac{2}{ln2}，+∞）$ |