题目内容
20.等差数列{an}的前n项和为${S_n}=\frac{{{n^2}+3n}}{2}$.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}满足${b_n}=\frac{1}{{{a_{2n-1}}{a_{2n+1}}}}$,求数列{bn}的前n项和Tn.
分析 (Ⅰ)根据数列的递推公式即可求出数列的通项公式,
(Ⅱ)化简数列{bn},再根据裂项求和即可求出
解答 解:(Ⅰ)当n=1时,a1=2,
当n≥2时,${a_n}={S_n}-{S_{n-1}}=\frac{{{n^2}+3n}}{2}-\frac{{{{(n-1)}^2}+3(n-1)}}{2}=n+1$,
数列{an}的通项公式为an=n+1;
(Ⅱ)${b_n}=\frac{1}{{{a_{2n-1}}{a_{2n+1}}}}=\frac{1}{(2n)(2n+2)}=\frac{1}{2}(\frac{1}{2n}-\frac{1}{2n+2})$,
${T_n}=\frac{1}{2}(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+…\frac{1}{2n}-\frac{1}{2n+2})=\frac{1}{2}(\frac{1}{2}-\frac{1}{2n+2})=\frac{n}{4n+4}$.
点评 本题考查了数列的递推公式和裂项求和,考查了学生的运算能力,属于中档题

练习册系列答案
相关题目
10.宁夏2011年起每年举办一届旅游节,到2016年已举办了六届,旅游部门统计在每届旅游节期间,吸引了不少外地游客到宁夏,这将极大地推进宁夏的旅游业的发展,现将前五届旅游节期间外地游客到宁夏的人数统计如下表:
(1)求y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$
(2)利用(1)中的线性回归方程,预测17年第7届旅游节期间外地游客到宁夏的人数.
| 年份 | 11年 | 12年 | 13年 | 14年 | 15年 |
| 旅游节届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$
(2)利用(1)中的线性回归方程,预测17年第7届旅游节期间外地游客到宁夏的人数.
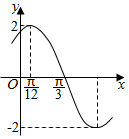 函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,
函数$f(x)=Asin({ωx+ϕ})({A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,