题目内容
13．函数$y=\frac{x^2}{2^x}$的单调增区间是（ ）| A． | $（0，\frac{2}{ln2}）$ | B． | $（-∞，0），（\frac{2}{ln2}，+∞）$ | C． | $（-∞，\frac{2}{ln2}）$ | D． | $（\frac{2}{ln2}，+∞）$ |
分析 利用导数判断函数的单调性求得单调区间即可．
解答 解：∵y′=$\frac{2x•{2}^{x}-{x}^{2}•{2}^{x}ln2}{{2}^{2x}}$=$\frac{2x-{x}^{2}ln2}{{2}^{x}}$=$\frac{x（2-xln2）}{{2}^{x}}$，函数$y=\frac{x^2}{2^x}$的单调递增，
∴x（2-xln2）＞0，
解得0＜x＜$\frac{2}{ln2}$，
故函数的单调递增区间为（0，$\frac{2}{ln2}$），
故选：A
点评 本题考查利用导数求函数的单调区间知识，属基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
3．设函数y=f（x）在x=x0处可导，且f′（x0）=1，则$\underset{lim}{n→∞}$C（x）=$\frac{f（{x}_{0}+2△x）-f（{x}_{0}）}{△x}$的值等于（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | 2 | D． | -2 |
4．已知A，B，C三点在球O的表面，△ABC是边长为5正三角形，球面上另外一点D到A，B，C三点的距离分别是3，4，5，则球O的表面积是（ ）
| A． | $\frac{100π}{3}$ | B． | $\frac{400π}{3}$ | C． | 100π | D． | 400π |
5．
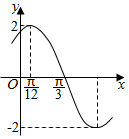函数$f（x）=Asin（{ωx+ϕ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，
求（Ⅰ）函数f（x）的解析式；
（Ⅱ）函数y=Acos（ωx+ϕ）的单调递增区间．
函数$f（x）=Asin（{ωx+ϕ}）（{A＞0，ω＞0，|φ|＜\frac{π}{2}}）$的部分图象如图所示，求（Ⅰ）函数f（x）的解析式；
（Ⅱ）函数y=Acos（ωx+ϕ）的单调递增区间．
2．已知$sin（-α）=\frac{{\sqrt{5}}}{3}$，则$cos（\frac{π}{2}+α）$的值为（ ）
| A． | $\frac{2}{3}$ | B． | $-\frac{2}{3}$ | C． | $\frac{{\sqrt{5}}}{3}$ | D． | $-\frac{{\sqrt{5}}}{3}$ |