题目内容
12.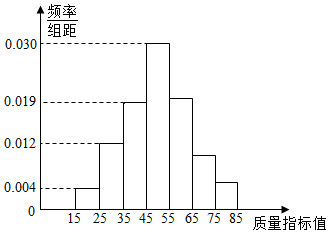 从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
从某企业生产的某种产品中抽取100件,测量这些产品的质量指标值,由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.(I)求这些产品质量指标值落在区间[75,85]内的频率;
(Ⅱ)若将频率视为概率,从该企业生产的这种产品中随机抽取3件,记这3件产品中质量指标值位于区间[45,75)内的产品件数为X,求X的分布列与数学期望.
分析 (I)由题意,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之和,利用之比为4:2:1,即可求出这些产品质量指标值落在区间[75,85]内的频率;
(Ⅱ)求出每件产品质量指标值落在区间[45,75)内的概率为0.6,利用题意可得:X~B(3,0.6),根据概率分布知识求解即可.
解答 解:(I)由题意,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之和为1-0.04-0.12-0.19-0.3=0.35,
∵质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1,
∴这些产品质量指标值落在区间[75,85]内的频率为0.05;
(Ⅱ)根据样本频率分布直方图,每件产品质量指标值落在区间[45,75)内的概率为0.6,
由题意可得:X~B(3,0.6)
∴X的概率分布列为
| X | 0 | 1 | 2 | 3 |
| P | 0.064 | 0.288 | 0.432 | 0.216 |
点评 本题考查概率分布在实际问题中的应用,结合了统计的知识,综合性较强,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知函数f(x)=xa的图象过点(4,2),令an=$\frac{1}{f(n+1)+f(n)}$,n∈N*,记数列{an}的前n项和为Sn,则S2014=( )
| A. | $\sqrt{2013}$-1 | B. | $\sqrt{2014}$-1 | C. | $\sqrt{2015}$-1 | D. | $\sqrt{2015}$+1 |
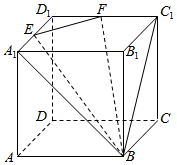 如图,已知正方体ABCD-A1B1C1D1的边长为2,点E,F分别是A1D1,C1D1的中点.
如图,已知正方体ABCD-A1B1C1D1的边长为2,点E,F分别是A1D1,C1D1的中点.