题目内容
二面角α-MN-β等于45°,A∈MN,P∈α,若∠PAN=45°,则AP与β所成的角是( )
分析:过点P作平面β的垂线PB,垂足为B,过点B作BC垂直于MN,连接PC,根据条件可以证得∠PCB为二面角α-MN-β的平面角,再分别在△PBA,△PCA,△PCB中,可求结论.
解答:解:过点P作平面β的垂线PB,垂足为B,过点B作BC垂直于MN,连接PC,则∠PAB为AP与β所成的角

∵PB⊥β,MN?β,∴PB⊥MN
∵MN⊥BC,∴∠PCB为二面角α-MN-β的平面角,∴∠PCB=45°,
设PB=1,在△PCB中,∠PCB=45°,∴PC=
在△PCA中,∠PAC=45°,∴PA=2
在△PBA中,sin∠PAB=
,∴∠PAB=30°
∴AP与β所成的角为30°
故选A.

∵PB⊥β,MN?β,∴PB⊥MN
∵MN⊥BC,∴∠PCB为二面角α-MN-β的平面角,∴∠PCB=45°,
设PB=1,在△PCB中,∠PCB=45°,∴PC=
| 2 |
在△PCA中,∠PAC=45°,∴PA=2
在△PBA中,sin∠PAB=
| 1 |
| 2 |
∴AP与β所成的角为30°
故选A.
点评:本题的考点是二面角的平面角及求法,主要考查利用定义找(作出)出二面角的平面角,关键是找(作出)出二面角的平面角,同时也考查学生计算能力.

练习册系列答案
相关题目
在等边三角形ABC中,M、N、P分别为AB、AC、BC的中点,沿MN将△AMN折起,使得面AMN与面MNCB所在二面角的余弦值为
,则直线AM与NP所成角的大小为( )
| 1 |
| 3 |
| A、90° | ||||
| B、60° | ||||
C、arccos
| ||||
D、arccos
|
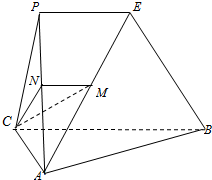 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥CB,M,N分别是线段AE,AP上的动点,且满足:
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥CB,M,N分别是线段AE,AP上的动点,且满足: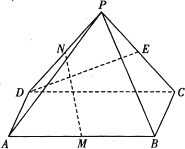 (2011•武汉模拟)如图,在四棱锥P-ABCD中,△PCD为等边三角形,四边形ABCD为矩形,平面PDC丄平面ABCD,M、N、E分别是AB、PD、PC的中点,AB=2AD.
(2011•武汉模拟)如图,在四棱锥P-ABCD中,△PCD为等边三角形,四边形ABCD为矩形,平面PDC丄平面ABCD,M、N、E分别是AB、PD、PC的中点,AB=2AD.