题目内容
在等边三角形ABC中,M、N、P分别为AB、AC、BC的中点,沿MN将△AMN折起,使得面AMN与面MNCB所在二面角的余弦值为
,则直线AM与NP所成角的大小为( )
| 1 |
| 3 |
| A、90° | ||||
| B、60° | ||||
C、arccos
| ||||
D、arccos
|
分析:根据翻折问题遵循的原则:翻折前后在同一个面上的位置关系及度量关系不变,求出各条线段的长及两面所成的角,将两条异面直线赋予向量意义,选出三个向量作为基底,将异面直线对应的向量用基底表示,求出这两个向量的数量积,根据向量垂直的充要条件求出两条异面直所成的角.
解答:解:设等边三角形ABC的边长为1,ME=
MN=
BC=
AE=EP=
AP=
且AE⊥MN,PE⊥MN
∴∠AEP为面AMN与面MNCB所在二面角的平面角
∴cos∠AEP=
∵
=
+
,
=
-
=
-
∴
•
=(
+
)•(
-
)
=
•
+
•
-
2-
•
=
•
-
2
=|
|
|cos∠AEP-
=
-
=0
∴
⊥
∴直线AM与NP所成角为90°
故选A
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
AE=EP=
| 1 |
| 2 |
| ||
| 4 |
且AE⊥MN,PE⊥MN
∴∠AEP为面AMN与面MNCB所在二面角的平面角
∴cos∠AEP=
| 1 |
| 3 |
∵
| MA |
| ME |
| EA |
| NP |
| EP |
| EN |
| EP |
| ME |
∴
| MA |
| NP |
| ME |
| EA |
| EP |
| ME |
=
| ME |
| EP |
| EA |
| EP |
| ME |
| EA |
| ME |
=
| EA |
| EP |
| ME |
=|
| EA| |
| EP |
| 1 |
| 16 |
=
| 1 |
| 16 |
| 1 |
| 16 |
∴
| MA |
| NP |
∴直线AM与NP所成角为90°
故选A
点评:求两条异面直线所成的角常借助的工具是向量,利用向量的数量积求出对应向量所成的角,再根据向量所成的角与异面直线所成角的关系求出;解决翻折问题应该先根据翻折问题遵循的原则:翻折前后在同一个面上的位置关系及度量关系不变找出空间图形的已知条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在等边三角形ABC中,AB=a,O为△ABC的中心,过O的直线交AB于M,交AC于N,求
在等边三角形ABC中,AB=a,O为△ABC的中心,过O的直线交AB于M,交AC于N,求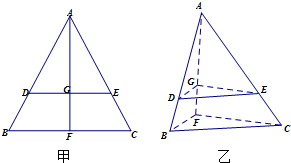 如图甲,在等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC上的点,AF与DE交于点G,将△ABF沿AF折起,得到如图乙所示的三棱锥A-BCF,证明:DE∥平面BCF.
如图甲,在等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC上的点,AF与DE交于点G,将△ABF沿AF折起,得到如图乙所示的三棱锥A-BCF,证明:DE∥平面BCF.