题目内容
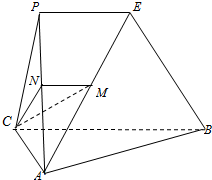如图，平面PAC⊥平面ABC，AC⊥BC，△PAC为等边三角形，PE∥CB，M，N分别是线段AE，AP上的动点，且满足：| AM |
| AE |
| AN |
| AP |
（Ⅰ）求证：MN∥平面ABC；
（Ⅱ）求λ的值，使得平面ABC与平面MNC所成的锐二面角的大小为45°．
分析：（Ⅰ） 证明：由
=
=λ，得MN∥PE，由线面平行的判定定理，所以MN∥平面ABC．
（Ⅱ）由（Ⅰ）知MN∥BC，故C、B、M、N共面，平面ABC与平面MNC所成的锐二面角即N-CB-A．所以∠NCA=45°．在△NCA中运用正弦定理得，λ=
-1
| AM |
| AE |
| AN |
| AP |
（Ⅱ）由（Ⅰ）知MN∥BC，故C、B、M、N共面，平面ABC与平面MNC所成的锐二面角即N-CB-A．所以∠NCA=45°．在△NCA中运用正弦定理得，λ=
| 3 |
解答：
解：（Ⅰ） 证明：由
=
=λ，得MN∥PE，
又依题意PE∥BC，所以MN∥BC．
因为MN?平面ABC，BC?平面ABC，
所以MN∥平面ABC．
（Ⅱ）由（Ⅰ）知MN∥BC，故C、B、M、N共面，平面ABC与平面MNC所成的锐二面角即N-CB-A．
因为平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，且CB⊥AC，
所以CB⊥平面PAC．故CB⊥CN，即知∠NCA为二面角N-CB-A的平面角．
所以∠NCA=45°．在△NCA中运用正弦定理得，
=
=
=
-1．
所以λ=
=
-1．
解：（Ⅰ） 证明：由| AM |
| AE |
| AN |
| AP |
又依题意PE∥BC，所以MN∥BC．
因为MN?平面ABC，BC?平面ABC，
所以MN∥平面ABC．
（Ⅱ）由（Ⅰ）知MN∥BC，故C、B、M、N共面，平面ABC与平面MNC所成的锐二面角即N-CB-A．
因为平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，且CB⊥AC，
所以CB⊥平面PAC．故CB⊥CN，即知∠NCA为二面角N-CB-A的平面角．
所以∠NCA=45°．在△NCA中运用正弦定理得，
| AN |
| AC |
| sin45° |
| sin75° |
| ||||||
|
| 3 |
所以λ=
| AN |
| AP |
| 3 |
点评：本题主要考查空间点、线、面位置关系，二面角等基础知识，空间向量的应用，同时考查空间想象能力和运算求解能力．
练习册系列答案
相关题目
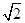倍，
倍，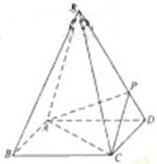
P为侧棱SD上的点。（Ⅰ）求证：AC⊥SD；