题目内容
已知函数f(x)=
x3+ax2-4x+4的图象关于点(0,4)对称.
(Ⅰ)求a的值;
(Ⅱ)求f(x)的极值;
(Ⅲ)求f(x)在区间[0,3]上的最大值与最小值.
| 1 |
| 3 |
(Ⅰ)求a的值;
(Ⅱ)求f(x)的极值;
(Ⅲ)求f(x)在区间[0,3]上的最大值与最小值.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)由已知条件得到f(x)+f(-x)=8,令x=1,能求出a的值.
(Ⅱ)f(x)=
x3-4x+4,f′(x)=x2-4=(x-2)(x+2),令f′(x)=0,得x=-2,x=2,由此列表讨论,能求出f(x)的极值.
(Ⅲ)由f(0)=4,f(3)=1,能求出f(x)在[0,3]上最大值和最小值.
(Ⅱ)f(x)=
| 1 |
| 3 |
(Ⅲ)由f(0)=4,f(3)=1,能求出f(x)在[0,3]上最大值和最小值.
解答:
解:(Ⅰ)∵函数y=f(x)的图象关于点(0,4)对称,
∴f(x)+f(-x)=8,
令x=1,得
+a-
+a+4+4=8,a=0.(3分)
(Ⅱ)f(x)=
x3-4x+4,f′(x)=x2-4=(x-2)(x+2),(4分)
令f′(x)=0,得x=-2,x=2,
当x<-2或x>2时,f′(x)>0;
当-2<x<2时,f′(x)<0,(6分)
(8分)
∴当x=-2时,f(x)有极大值,为f(-2)=
;
当x=2时,f(x)有极小值f(2)=-
.(10分)
(Ⅲ)∵f(0)=4,f(3)=1,
由(2)知f(x)在[0,3]上最大值是4,最小值是-
.(12分)
∴f(x)+f(-x)=8,
令x=1,得
| 1 |
| 3 |
| 1 |
| 3 |
(Ⅱ)f(x)=
| 1 |
| 3 |
令f′(x)=0,得x=-2,x=2,
当x<-2或x>2时,f′(x)>0;
当-2<x<2时,f′(x)<0,(6分)
| x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) | ||||
| f′(x) | + | 0 | - | 0 | + | ||||
| f(x) | ↗ |
|
↘ | -
|
↗ |
∴当x=-2时,f(x)有极大值,为f(-2)=
| 28 |
| 3 |
当x=2时,f(x)有极小值f(2)=-
| 4 |
| 3 |
(Ⅲ)∵f(0)=4,f(3)=1,
由(2)知f(x)在[0,3]上最大值是4,最小值是-
| 4 |
| 3 |
点评:本题考查函数的极值和最值的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在直角坐标系中,已知点A(0,1)和点B(-3,4),若点P在∠AOB的平分线上且|
|=2,则点P的坐标为( )
| OP |
A、(-
| ||||||||
B、(-
| ||||||||
C、(-
| ||||||||
D、(-
|
若函数f(x)在给定区间M上存在正数t,使得对于任意的x∈M,有x+t∈M,且f(x+t)≥f(x),则称f(x)为M上t级类增函数,则下列命题中正确的是( )
A、函数f(x)=
| ||||||
| B、函数f(x)=|log2(x-1)|是(1,+∞)上的1级类增函数 | ||||||
C、若函数f(x)=sinx+ax为[
| ||||||
| D、若函数f(x)=x2-3x为[1,+∞)上的t级类增函数,则实数t的取值范围为[2,+∞) |
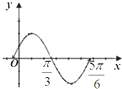
已知函数y=2sin(ωx+φ)(ω>0,|φ|<
)的图象的一部分如图所示,则( )
| π |
| 2 |

A、ω=2,φ=
| ||
B、ω=2,φ=-
| ||
C、ω=2,φ=
| ||
D、ω=2,φ=-
|
已知直线的倾斜角的余弦值是
,则此直线的斜率是( )
| 1 |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、±
|
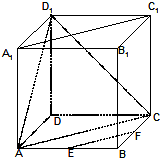 如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别为棱AB,BC的中点.
如图,棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别为棱AB,BC的中点.