题目内容
6.已知函数f(x)(x∈D),若存在常数T(T>0),对任意x∈D都有f(x+T)=T•f(x),则称函数f(x)为T倍周期函数(1)判断h(x)=x是否是T倍周期函数,并说明理由;
(2)证明:g(x)=($\frac{1}{4}$)x是T倍周期函数,且T的值是唯一的;
(3)若f(n)(n∈N*)是2倍周期函数,f(1)=1,f(2)=-4,Sn表示f(n)的前n 项和,Cn=$\frac{{S}_{2n}}{{S}_{2n-1}}$,求$\underset{lim}{n→∞}$Cn.
分析 (1)假设设h(x+T)=T•h(x)进而得出结论;
(2)通过设g(x+T)=T•g(x)并令x=0可知T=$\frac{1}{2}$,分T>$\frac{1}{2}$、T<$\frac{1}{2}$两种情况证明唯一性即可;
(3)利用f(n+2)=2•f(n)及f(1)=1、f(2)=-4分别计算出n为奇数、偶数时的值,进而利用等比数列的求和公式计算可知S2n=-3(2n-1)、S2n-1=-2n+3,计算即得结论.
解答 (1)结论:h(x)=x不是T倍周期函数.
理由如下:
依题意,设h(x+T)=T•h(x),则x+T=T•x对任意x恒成立,
∵T无解,
∴h(x)=x不是T倍周期函数;
(2)证明:设g(x+T)=T•g(x),则$(\frac{1}{4})^{x+T}$=T•$(\frac{1}{4})^{x}$对任意x恒成立,
令x=0,得$(\frac{1}{4})^{T}$=T,即T=$\frac{1}{2}$;
下证唯一性:
若T>$\frac{1}{2}$,T=$(\frac{1}{4})^{T}$<$(\frac{1}{4})^{\frac{1}{2}}$=$\frac{1}{2}$,矛盾;
若T<$\frac{1}{2}$,T=$(\frac{1}{4})^{T}$>$(\frac{1}{4})^{\frac{1}{2}}$=$\frac{1}{2}$,矛盾;
∴T=$\frac{1}{2}$是唯一的;
(3)解:依题意,f(3)=f(1+2)=2f(1)=2,
f(5)=f(3+2)=2f(3)=22,
f(7)=f(5+2)=2f(5)=23,
…
f(2n-1)=f(2n-3+2)=2f(2n-3)=2n-1,
∴f(1)+f(3)+…f(2n-1)=1+2+22+…+2n-1=2n-1,
同理可得:f(2)+f(4)+…+f(2n)=-4(1+2+22+…+2n-1)=-4(2n-1),
∴S2n=f(1)+f(2)+…+f(2n)=-3(2n-1),
同理S2n-1=f(1)+f(2)+…+f(2n-1)=-2n+3,
∴$\underset{lim}{n→∞}$Cn=$\underset{lim}{n→∞}$$\frac{{S}_{2n}}{{S}_{2n-1}}$=$\underset{lim}{n→∞}$$\frac{3({2}^{n}-1)}{{2}^{n}-3}$=3.
点评 本题考查数列的求和与极限,考查分类讨论的思想,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案(1)若从第6行第7列的数开始右读,请你一次写出最先抽出的5个人的编号(下面是摘自随机数表的第4恒值第7行);
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
(2)抽出的100名学生的数学、外语成绩如下表:
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
(3)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
| A. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{12}=1(x>2)$ | C. | y2=8x | D. | y2=8x(x≠0) |
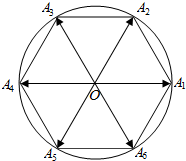 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$. 如图,点A、B分别是角α、β的终边与单位圆的交点,$0<β<\frac{π}{2}<α<π$.
如图,点A、B分别是角α、β的终边与单位圆的交点,$0<β<\frac{π}{2}<α<π$.