题目内容
11.不等式-x2+4x-4<0的解集为( )| A. | R | B. | Φ | C. | (-∞,2)∪(2,+∞) | D. | {2} |
分析 把不等式化为x2-4x+4>0,即(x-2)2>0,写出不等式的解集即可.
解答 解:不等式-x2+4x-4<0可化为x2-4x+4>0,
即(x-2)2>0,
所以不等式的解集为(-∞,2)∪(2,+∞).
故选:C.
点评 本题考查了一元二次不等式的解集问题,是基础题目.

练习册系列答案
相关题目
19.复数z=i(2-i)(i是虚数单位),则z的共轭复数$\overline z$=( )
| A. | 1-2i | B. | 1+2i | C. | -1+2i | D. | -1-2i |
16.已知在三角形ABC中,AB=AC,BC=4,∠BAC=120°,$\overrightarrow{BE}$=3$\overrightarrow{EC}$,若P是BC边上的动点,则$\overrightarrow{AP}$•$\overrightarrow{AE}$的取值范围是( )
| A. | [-1,3] | B. | $[{-\frac{2}{3},3}]$ | C. | $[{-\frac{2}{3},\frac{10}{3}}]$ | D. | $[{-1,\frac{10}{3}}]$ |
3.广州某社区对居民进行垃圾分类知识知晓情况的分层抽样调查.已知该社区的青年人、中年人和老年人分别有800人、1600人、1400人,若在老年人中的抽样人数是70,则在青年人中的抽样人数是( )
| A. | 20 | B. | 40 | C. | 60 | D. | 80 |
20.中国柳州从2011年起每年国庆期间都举办一届国际水上狂欢节,到2016年已举办了六届,旅游部门统计在每届水上狂欢节期间,吸引了不少外地游客到柳州,这将极大地推进柳州的旅游业的发展,现将前五届水上狂欢节期间外地游客到柳州的人数统计表如表:
(1)求y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)旅游部门统计在每届水上狂欢节期间,每位外地游客可为本市增加100元左右的旅游收入,利用(1)中的线性回归方程,预测2017年第7届柳州国际水上狂欢节期间外地游客可为本市增加的旅游收入达多少?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
| 份(x) | 2011年 | 2012年 | 2013年 | 2014年 | 2015年 |
| 水上狂欢节届编号x | 1 | 2 | 3 | 4 | 5 |
| 外地游客人数y(单位:十万) | 0.6 | 0.8 | 0.9 | 1.2 | 1.5 |
(2)旅游部门统计在每届水上狂欢节期间,每位外地游客可为本市增加100元左右的旅游收入,利用(1)中的线性回归方程,预测2017年第7届柳州国际水上狂欢节期间外地游客可为本市增加的旅游收入达多少?
$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x.
1.若复数z满足(1-z)(1+2i)=i,则在复平面内表示复数z的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
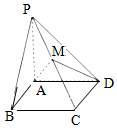 已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.
已知四棱锥P-ABCD中,底面为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC上一点,M为PC的中点.