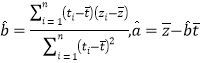题目内容
【题目】已知椭圆![]() 中心在原点,焦点在
中心在原点,焦点在![]() 轴上,且其焦点和短轴端点都在圆
轴上,且其焦点和短轴端点都在圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)点![]() 是圆
是圆![]() 上一点,过点
上一点,过点![]() 作圆
作圆![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() ,
,![]() 两点,求
两点,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)2
;(2)2
【解析】
(1)由题意设出椭圆的标准方程,由于椭圆焦点和短轴端点都在圆![]() :
:![]() 上,可得到
上,可得到![]() ,
,![]() 的值,即可求出椭圆方程。
的值,即可求出椭圆方程。
(2)分类讨论切线方程斜率存在与不存在的情况,当斜率不存在时,可直接确定![]() 的值,再讨论斜率存在时,设出直线方程与椭圆方程联立,利用韦达定理表示出
的值,再讨论斜率存在时,设出直线方程与椭圆方程联立,利用韦达定理表示出![]() ,再结合直线与圆相切性质消去一个参数,利用函数的单调性确定
,再结合直线与圆相切性质消去一个参数,利用函数的单调性确定![]() 的范围,最后得到
的范围,最后得到![]() 的最大值。
的最大值。
(1)由椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,故设椭圆
轴上,故设椭圆![]() 的标准方程为
的标准方程为![]() ,
,
![]() 椭圆的右焦点坐标为
椭圆的右焦点坐标为![]() ,上顶点坐标为
,上顶点坐标为![]()
![]() 椭圆
椭圆![]() 焦点和短轴端点都在圆
焦点和短轴端点都在圆![]() :
:![]() 上,
上,
![]()
![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,
,
![]()
![]() ,即
,即![]() ,
,
椭圆![]() 的标准方程为
的标准方程为![]()
(2)当切线![]() 的斜率不存在时,切线方程为:
的斜率不存在时,切线方程为:![]() ,与椭圆
,与椭圆![]() 的两个交点为
的两个交点为![]() 或
或![]() ,则
,则![]() ,
,
当切线![]() 的斜率存在时,设切线方程为:
的斜率存在时,设切线方程为:![]() ,切线与椭圆交点的坐标分别为
,切线与椭圆交点的坐标分别为![]() ,
,![]() ,
,
联立方程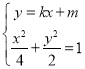 ,得:
,得:![]() ,
,
由于切线与椭圆相交于两点,则![]() ,
,
由韦达定理可得: ,
,
又![]() 直线
直线![]() 与圆
与圆![]() 相切,
相切,
![]()
![]() ,即
,即![]() ,
,
![]()
![]()
![]()
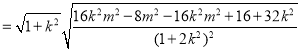




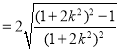
![]()
令![]() ,则函数
,则函数![]() 单调递增,当
单调递增,当![]() ,
,![]()
![]()
![]() ,
,
综上所述,![]()

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
【题目】高一学年结束后,要对某班的50名学生进行文理分班,为了解数学对学生选择文理科是否有影响,有人对该班的分科情况做了如下的数据统计:
理科人数 | 文科人数 | 总计 | |
数学成绩好的人数 | 25 | 30 | |
数学成绩差的人数 | 10 | ||
合计 | 15 |
(Ⅰ)根据数据关系,完成![]() 列联表;
列联表;
(Ⅱ)通过计算判断能否在犯错误的概率不超过![]() 的前提下认为数学对学生选择文理科有影响.
的前提下认为数学对学生选择文理科有影响.
附:![]()
| 0.05 | 0.025 | 0.010 | 0.005 |
| 3.841 | 5.024 | 6.635 | 7.879 |