Question

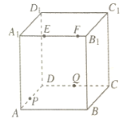
【题目】如图，正方体的棱长为4，动点E，F在棱上，动点P，Q分别在棱AD，CD上。若，，，（大于零），则四面体PEFQ的体积

A.与都有关B.与m有关，与无关

C.与p有关，与无关D.与π有关，与无关

Answer 1

【答案】C

【解析】

连接、交于点，作，证明平面，可得出平面，于此得出三棱锥的高为，再由四边形为矩形知，点到的距离为，于此可计算出的面积为，最后利用锥体的体积公式可得出四面体的体积的表达式，于此可得出结论。

如下图所示，连接、交于点，作，

在正方体中，平面，且平面，

，又四边形为正方形，则，且，

平面，即平面，，平面，

且，

易知四边形是矩形，且，点到直线的距离为，

的面积为，

所以，四面体的体积为，

因此，四面体的体积与有关，与、无关，故选：C.