题目内容

10．已知函数f（x）是定义在R上的奇函数．当x≥0时，f（x）=2x+t（t为常数）．则f（m）＜3成立的一个充分不必要条件是（　　）
A．m＜3B．m＜2C．-2＜m＜2D．m＞2

分析 根据函数f（x）是定义在R上的奇函数，可得f（0）=0，求出参数t后，分析函数的单调性，可得f（m）＜3成立的充要条件，进而得到答案．

解答 解：∵函数f（x）是定义在R上的奇函数．
∴f（0）=20+t=1+t=0，
解得：t=-1，
∴当x≥0时，f（x）=2x-1，为增函数，
∴函数f（x）是定义在R上的增函数，
令f（m）=3，则m=2，
∴解f（m）＜3得：m＜2，
故四个答案中-2＜m＜2是f（m）＜3成立的一个充分不必要条件，
故选：C

点评 本题考查的知识点是函数的奇偶性，函数的单调性，充要条件，是逻辑与函数的综合应用，难度中档．

练习册系列答案
相关题目
8．已知实数x、y满足$\sqrt{x+3y}$$•\sqrt{x-3y}$=3，则x-|y|的最小值是2$\sqrt{2}$．
1．设M为平面上以A（4，1），B（-1，-6），C（-3，2）三点为顶点的三角形区域（包括内部和边界），当点（x，y）在M上变化时，z=4x-3y的取值范围是（　　）
A．[-18，13]B．[0，14]C．[13，14]D．[-18，14]
18．已知函数f（x）=a•（$\frac{1}{3}$）x+bx2+cx（a∈R，b≠0，c∈R），若{x|f（x）=0}={x|f（f（x））=0}≠∅，则实数c的取值范围为[0，4）．
5．15名选举人对5名侯选人进行无记名投票选举，若选举人可以投一个至五个候选人的票，也可以弃权，则不同的选举方法共有（　　）
A．215种B．275种C．25种D．225种
15．已知$f（x）=\sqrt{4-{x^2}}$，g（x）=|x-2|，则下列函数中是奇函数的为（　　）
A．h（x）=f（x）+g（x）B．h（x）=f（x）•g（x）C．$h（x）=\frac{g（x）}{2-f（x）}$D．$h（x）=\frac{f（x）}{2-g（x）}$
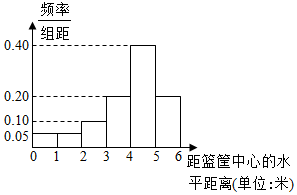2．某篮球队对篮球运动员的篮球技能进行统计研究，针对篮球运动员在投篮命中时，运动员在篮筐中心的水平距离这项指标，对某运动员进行了若干场次的统计，依据统计结果绘制如下频率分布直方图：
（Ⅰ）依据频率分布直方图估算该运动员投篮命中时，他到篮筐中心的水平距离的中位数；
（Ⅱ）若从该运动员投篮命中时，他到篮筐中心的水平距离为2到5米的这三组中，用分层抽样的方法抽取7次成绩（单位：米，运动员投篮命中时，他到篮筐中心的水平距离越远越好），并从抽到的这7次成绩中随机抽取2次．规定：这2次成绩均来自到篮筐中心的水平距离为4到5米的这一组，记1分，否则记0分．求该运动员得1分的概率．
19．下列函数中在$（\frac{π}{4}，\frac{3}{4}π）$上为减函数的是（　　）
A．y=2cos2x-1B．y=-tanxC．$y=cos（2x-\frac{π}{2}）$D．y=sin2x+cos2x
20．记max{a，b}=$\left\{\begin{array}{l}{a，}&{a≥b}\\{b，}&{a＜b}\end{array}\right.$，则f（x）=max{sinx，cosx}的值域[-$\frac{\sqrt{2}}{2}$，1]，周期为2π，单调增区间为[2kπ+$\frac{π}{4}$，2kπ+$\frac{π}{2}$]，[2kπ-$\frac{3π}{4}$，2kπ+$\frac{π}{4}$]，（k∈Z）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网