题目内容
8.已知实数x、y满足$\sqrt{x+3y}$$•\sqrt{x-3y}$=3,则x-|y|的最小值是2$\sqrt{2}$.分析 由题意可得x+3y≥0,x-3y≥0,即有x2-9y2=9(x>0),令x-|y|=t,即有|y|=x-t,代入双曲线的方程,运用判别式非负,解不等式即可得到最小值.
解答 解:由$\sqrt{x+3y}$$•\sqrt{x-3y}$=3,可得
x+3y≥0,x-3y≥0,即有x2-9y2=9(x>0),
令x-|y|=t,即有|y|=x-t,
可得y2=(x-t)2,代入x2-9y2=9(x>0),
即有8x2-18tx+9t2+9=0,
由x>0可得t>0,
由△=324t2-32(9t2+9)≥0,
解得t2≥8,解得t≥2$\sqrt{2}$.
即有x=$\frac{9\sqrt{2}}{4}$,y=±$\frac{\sqrt{2}}{4}$,x-|y|取得最小值2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查最值的求法,注意运用转化思想和二次方程的判别式法,考查化简整理的运算能力,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
18.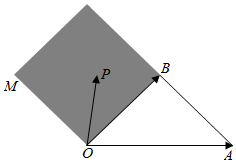 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )
 如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )
如图,OM∥AB,点P在由射线OM,线段OB及AB的延长线围成的阴影区域内(不含边界),且$\overrightarrow{OP}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$,则实数对(x,y)可以是( )| A. | ($\frac{1}{4}$,$\frac{3}{4}$) | B. | (-$\frac{2}{3}$,$\frac{2}{3}$) | C. | (-$\frac{1}{4}$,$\frac{3}{4}$) | D. | (-$\frac{1}{5}$,$\frac{7}{5}$) |
12.已知命题p:函数y=2-ax+1的图象恒过定点(1,2);命题q:若函数y=f(x-1)为偶函数,则函数y=f(x)的图象关于直线x=1对称,则下列命题为真命题的是( )
| A. | p∨q | B. | p∧q | C. | ¬p∧q | D. | p∨¬q |
10.已知函数f(x)是定义在R上的奇函数.当x≥0时,f(x)=2x+t(t为常数).则f(m)<3成立的一个充分不必要条件是( )
| A. | m<3 | B. | m<2 | C. | -2<m<2 | D. | m>2 |