题目内容
2.点G是△ABC的重心,$|{\overrightarrow{AC}}|=1,|{\overrightarrow{BC}}|=\sqrt{2}$,且AG⊥BG,则sinC=$\frac{4}{5}$.分析 设GE=y,GF=x,由三角形重心的性质及勾股定理可得:x2+(2y)2=$\frac{1}{4}$,(2x)2+y2=$\frac{1}{2}$,解得x2,y2,利用勾股定理可求c2,由余弦定理可得cosC的值,进而利用同角三角函数基本关系式可求sinC的值.
解答 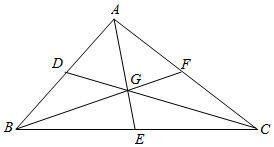 解:由已知,AF=$\frac{1}{2}$,BE=$\frac{\sqrt{2}}{2}$,
解:由已知,AF=$\frac{1}{2}$,BE=$\frac{\sqrt{2}}{2}$,
设GE=y,GF=x,则:AG=2y,BG=2x,
由勾股定理可得:x2+(2y)2=$\frac{1}{4}$,(2x)2+y2=$\frac{1}{2}$,
解得:x2=$\frac{7}{60}$,y2=$\frac{1}{30}$,
可得:c2=AB2=(2x)2+(2y)2=$\frac{3}{5}$,
由余弦定理可得:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{2+1-\frac{3}{5}}{2×2×1}$=$\frac{3}{5}$,
可得:sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题主要考查了三角形重心的性质及勾股定理,余弦定理,同角三角函数基本关系式在解三角形中的综合应用,考查了计算能力和转化思想,考查了数形结合思想,属于中档题.

练习册系列答案
相关题目
13.已知函数f(x)=x3+x2f'(2),则f'(2)的值为( )
| A. | -4 | B. | 4 | C. | -3 | D. | 3 |
11.△ABC中,AB=3,BC=2,CA=$\sqrt{19}$,若点D满足$\overrightarrow{BD}$=3$\overrightarrow{DC}$,则△ABD的面积为( )
| A. | $\frac{9\sqrt{3}}{8}$ | B. | $\frac{9}{8}$ | C. | 9$\sqrt{3}$ | D. | 12 |
15.记凸n(n≥3)边形的对角线的条数为f(n),则f(n)的表达式为( )
| A. | f(n)=n+1 | B. | f(n)=2n-1 | C. | $f(n)=\frac{{n({n-3})}}{2}$ | D. | $f(n)=\frac{{n({n+1})}}{2}$ |