题目内容
1.已知函数为奇函数,且f($\frac{π}{4}$)=0,其中a∈R,θ∈(0,π),f(x)=(a+2cos2x)cos(2x+θ).(1)求a,θ的值;
(2)若f($\frac{a}{4}$)=-$\frac{2}{5}$,α∈($\frac{π}{2}$,π),求sin(α+$\frac{π}{3}$)的值.
分析 (1)把x=$\frac{π}{4}$代入函数解析式可求得a的值,进而根据函数为奇函数推断出f(0)=0,进而求得cosθ,则θ的值可得.
(2)利用f($\frac{α}{4}$)=-$\frac{2}{5}$和函数的解析式可求得sinα,cosα,最后利用两角和与差的正弦公式求得答案.
解答 解:(1)f($\frac{π}{4}$)=-(a+1)sinθ=0,
∵θ∈(0,π).
∴sinθ≠0,
∴a+1=0,即a=-1,
∵f(x)为奇函数,
∴f(0)=(a+2)cosθ=0,
∴cosθ=0,θ=$\frac{π}{2}$.
(2)由(1)知f(x)=(-1+2cos2x)cos(2x+$\frac{π}{2}$)=cos2x•(-sin2x)=-$\frac{1}{2}sin4x$,
∴f($\frac{α}{4}$)=-$\frac{1}{2}$sinα=-$\frac{2}{5}$,
∴sinα=$\frac{4}{5}$,
∵α∈($\frac{π}{2}$,π),
∴cosα=-$\frac{3}{5}$,
∴sin(α+$\frac{π}{3}$)=sinαcos$\frac{π}{3}$+cosαsin$\frac{π}{3}$=$\frac{4-3\sqrt{3}}{10}$.
点评 本题主要考查了同角三角函数关系,三角函数恒等变换的应用,函数奇偶性问题.综合运用了所学知识解决问题的能力.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
11.若满足$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$的x,y使得不等式2x+y+m>0恒成立,则m的取值范围是( )
| A. | m<-3 | B. | m>3 | C. | m<3 | D. | m>-3 |
16.已知sinα=$\frac{\sqrt{5}}{5}$,则cos(α-$\frac{π}{4}$)的值为( )
| A. | $\frac{3\sqrt{10}}{10}$ | B. | -$\frac{\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$或-$\frac{\sqrt{10}}{10}$ |
3.已知G,N,P在△ABC所在平面内,a,b,c分别为角A,B,C所对的边,且分别满足$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,sin2A•$\overrightarrow{NA}$+sin2B•$\overrightarrow{NB}$+sin2C•$\overrightarrow{NC}$=$\overrightarrow{0}$,a$\overrightarrow{PA}$+b$\overrightarrow{PB}$+c$\overrightarrow{PC}$=$\overrightarrow 0$,则点G,N,P依次是△ABC的( )
| A. | 重心,外心,内心 | B. | 重心,垂心,内心 | C. | 重心,垂心,外心 | D. | 内心,外心,重心 |
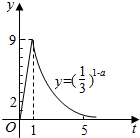 我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线