题目内容
点P(x,y)是椭圆6x2+3y2=12上的一个动点,则x+2y的最大值为( )
A、2
| ||
B、3
| ||
C、2
| ||
D、3
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由椭圆方程化为标准方程,设x=
cosθ,y=2sinθ,利用两角和差的正弦公式及正弦函数的单调性即可得出
| 2 |
解答:
解:由椭圆6x2+3y2=12化为
+
=1,
设x=
cosθ,y=2sinθ,
∴x+2y=
cosθ+4sinθ=3
sin(θ+α)(tanα=
).
∴x+2y的最大值为3
.
故选:B.
| x2 |
| 2 |
| y2 |
| 4 |
设x=
| 2 |
∴x+2y=
| 2 |
| 2 |
| ||
| 2 |
∴x+2y的最大值为3
| 2 |
故选:B.
点评:本题考查了椭圆的标准方程、两角和差的正弦公式及正弦函数的单调性,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
设复数z=
(i为虚数单位),则z的虚部为( )
| 2 |
| 1+i |
| A、-i | B、i | C、-1 | D、1 |
已知函数f(x)=
,若函数y=f(x+m)-
为奇函数,则实数m为( )
| 1 |
| 4x+2 |
| 1 |
| 4 |
A、-
| ||
| B、0 | ||
C、
| ||
| D、1 |
已知集合A={x|y=
},B={y|y=2x,x>0},则A∪B=( )
| 9-x2 |
| A、{x|x>1} |
| B、{x|1<x≤3} |
| C、{x|x≥-3} |
| D、∅ |
函数y=ln(2x2+1)的导数是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f(n)=
,且an=f(n)+f(n+1),则a1+a2+…+a2014的值为( )
|
| A、0 | B、2014 |
| C、-2014 | D、2014×2015 |
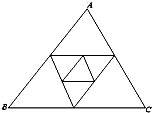 如图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,设第n个三角形周长为l(n),则归纳l(n)关于n的表达式为l(n)=
如图,已知△ABC周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,设第n个三角形周长为l(n),则归纳l(n)关于n的表达式为l(n)=