题目内容
设a、b、c均为正数.求证：
≥
.
证明略
解析:
证明 方法一 ∵
+3
=
=(a+b+c) 
=
［(a+b)+(a+c)+(b+c)］
≥ (
·
+
·
+
·
)2=
.∴
+
≥.
方法二 令
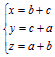,则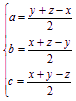
∴左边=
≥
=.
∴原不等式成立.
练习册系列答案
相关题目
设a，b，c均为正数，且2a=log
a，(
)b=log
b，(
)c=log2c，则（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a＜b＜c |
| B、c＜b＜a |
| C、c＜a＜b |
| D、b＜a＜c |