题目内容
某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示:
(1)请计算第几天该商品的销售单价为35元/件?
(2)求该网店第x天获得的利润y关于x的函数关系式;
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?
| 销售量P(件) | p=50-x | ||||
| 销售单价q(元/件) | 当1≤x≤20时,q=30+
当21≤x≤40时,q=20+
|
(2)求该网店第x天获得的利润y关于x的函数关系式;
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?
考点:函数模型的选择与应用,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)讨论x的取值范围,即可得到结论.
(2)根据条件建立函数关系式,即可求该网店第x天获得的利润y关于x的函数关系式;
(3)根据分段函数的性质,即可求出函数的最值.
(2)根据条件建立函数关系式,即可求该网店第x天获得的利润y关于x的函数关系式;
(3)根据分段函数的性质,即可求出函数的最值.
解答:
解:(1)当1≤x≤20时,q=30+
x=35,解得:x=10,
当21≤x≤40时,q=30+
=35,解得:x=35,
∴第10天或第35天该商品的销售单价为35元/件.
(2)当1≤x≤20时,y=(30+
x-20)(50-x)=-
x2+15x+500,
当21≤x≤40时,y=(20+
-20)(50-x)=
-525,
∴y关于x的函数关系式为y=
.
(3)当1≤x≤20时,y=-
x2+15x+500=-
(x-15)2+612.5,
∴当x=15时,y有最大值为612.5,
当21≤x≤40时,y=
-525是减函数,
∴当x=21时,y有最大值为725,
∵725>612.5,
∴这40天中该网店第21天获得的利润最大,最大为725元.
| 1 |
| 2 |
当21≤x≤40时,q=30+
| 525 |
| x |
∴第10天或第35天该商品的销售单价为35元/件.
(2)当1≤x≤20时,y=(30+
| 1 |
| 2 |
| 1 |
| 2 |
当21≤x≤40时,y=(20+
| 525 |
| x |
| 26250 |
| x |
∴y关于x的函数关系式为y=
|
(3)当1≤x≤20时,y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=15时,y有最大值为612.5,
当21≤x≤40时,y=
| 26250 |
| x |
∴当x=21时,y有最大值为725,
∵725>612.5,
∴这40天中该网店第21天获得的利润最大,最大为725元.
点评:本题主要考查函数的应用问题,根据条件建立函数关系,利用函数单调性的性质是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
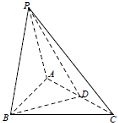 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.