题目内容
设f(x)=ex(ax2+3),其中a为实数.
(1)当a=-1时,求f(x)的极值;
(2)若f(x)为[1,2]上的单调函数,求a的取值范围.
(1)当a=-1时,求f(x)的极值;
(2)若f(x)为[1,2]上的单调函数,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:计算题,导数的综合应用
分析:(1)当a=-1时,有f(x)=ex(-x2+3),求导确定函数的单调性,由单调性求极值;
(2)要使f(x)为[1,2]上的单调函数,则f′(x)=ex(ax2+2ax+3)≥0或f′(x)=ex(ax2+2ax+3)≤0恒成立,从而转化为最值问题.
(2)要使f(x)为[1,2]上的单调函数,则f′(x)=ex(ax2+2ax+3)≥0或f′(x)=ex(ax2+2ax+3)≤0恒成立,从而转化为最值问题.
解答:
解:(1)当a=-1时,有f(x)=ex(-x2+3),
f′(x)=ex(-x2+3)-2xex
=-ex(x+3)(x-1),
由f′(x)>0得,x∈(-3,1),
故f(x)在(-3,1)上单调递增,
由f′(x)<0得,x∈(-∞,-3),(1,+∞),
故f(x)在(-∞,-3),(1,+∞),上单调递减,
∴f极小值(x)=f(-3)=-6e-3,f极小值(x)=f(1)=2e.
(2)要使f(x)为[1,2]上的单调函数,
则f′(x)=ex(ax2+2ax+3)≥0或
f′(x)=ex(ax2+2ax+3)≤0恒成立,
即a≥(
)max=-
,
或a≤(
)min=-1,
故a≥-
或a≤-1.
f′(x)=ex(-x2+3)-2xex
=-ex(x+3)(x-1),
由f′(x)>0得,x∈(-3,1),
故f(x)在(-3,1)上单调递增,
由f′(x)<0得,x∈(-∞,-3),(1,+∞),
故f(x)在(-∞,-3),(1,+∞),上单调递减,
∴f极小值(x)=f(-3)=-6e-3,f极小值(x)=f(1)=2e.
(2)要使f(x)为[1,2]上的单调函数,
则f′(x)=ex(ax2+2ax+3)≥0或
f′(x)=ex(ax2+2ax+3)≤0恒成立,
即a≥(
| -3 |
| x2+2x |
| 3 |
| 8 |
或a≤(
| -3 |
| x2+2x |
故a≥-
| 3 |
| 8 |
点评:本题考查了导数的综合应用,同时考查了恒成立问题的处理方法,属于中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
设M是△ABC边BC上任意一点,N为AM上一点且AN=2NM,若
=λ
+μ
,则λ+μ=( )
| AN |
| AB |
| AC |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
已知平面向量
,
满足|
|=1,|
|=2,且(
+
)⊥
,则
与
的夹角是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
| ∫ |
-
|
| x |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、π+
|
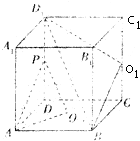 如图,在正方形ABD-A1B1C1D1,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点.求证:
如图,在正方形ABD-A1B1C1D1,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的中点.求证: