题目内容
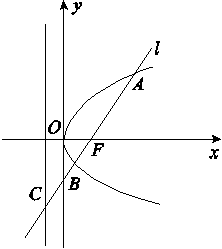
过抛物线y2=2px(p>0)焦点F的直线l与抛物线交于B,C两点,l与抛物线的准线交于点A,且|AF|=6, =2
=2 ,则|BC|=( )
,则|BC|=( )
A. B.6 C.
B.6 C. D.8
D.8
A
[解析] 不妨设直线l的倾斜角为θ,其中0<θ< ,点B(x1,y1),C(x2,y2),则点B在x轴的上方.过点B作该抛物线的准线的垂线,垂足为B1,于是有|BF|=|BB1|=3,
,点B(x1,y1),C(x2,y2),则点B在x轴的上方.过点B作该抛物线的准线的垂线,垂足为B1,于是有|BF|=|BB1|=3, =
= ,由此得p=2,抛物线方程为y2=4x,焦点F(1,0),cos θ=
,由此得p=2,抛物线方程为y2=4x,焦点F(1,0),cos θ= =
= =
= =
= ,sin θ=
,sin θ=  =
= ,tan θ=
,tan θ= =2
=2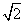 ,直线l:y=2
,直线l:y=2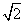 (x-1).由
(x-1).由 得8(x-1)2=4x,即2x2-5x+2=0,x1+x2=
得8(x-1)2=4x,即2x2-5x+2=0,x1+x2= ,|BC|=x1+x2+p=
,|BC|=x1+x2+p= +2=
+2= ,故选A.
,故选A.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:
表1 市场供给量
| 单价 (元/kg) | 2 | 2.4 | 2.8 | 3.2 | 3.6 | 4 |
| 供给量
| 50 | 60 | 70 | 75 | 80 | 90 |
表2 市场需求量
| 单价 (元/kg) | 4 | 3.4 | 2.9 | 2.6 | 2.3 | 2 |
| 需求量 (1000kg) | 50 | 60 | 65] | 70 | 75 | 80 |
根据以上提供的信息,市场供需平衡点(即供给量和需求量相等时的单价)应在区间(C )
A.[2.3,2.6]内 B.[2.4,2.6]内  C.[2.6,2.8
C.[2.6,2.8 ]内 D.[2.8,2.9]内
]内 D.[2.8,2.9]内
 ,则满足
,则满足 的
的 的值为____________
的值为____________ ,则
,则 ”是
”是 (1000kg)
(1000kg)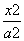 -
-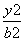 =1(a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为30°的直线交双曲线右支于M点,若MF2⊥x轴,则双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点分别是F1,F2,过F1作倾斜角为30°的直线交双曲线右支于M点,若MF2⊥x轴,则双曲线的离心率为( )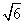 B.
B.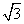
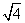 D.
D.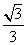
 =1与椭圆C2的公共焦点,点A是C1,C2在第一象限的公共点.若|F1F2|=|F1A|,则C2的离心率是( )
=1与椭圆C2的公共焦点,点A是C1,C2在第一象限的公共点.若|F1F2|=|F1A|,则C2的离心率是( )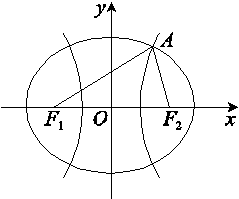
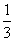 B.
B.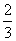
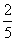 D.
D.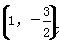 在椭圆C:
在椭圆C: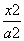 +
+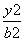 =1(a>b>0)上,过椭圆C的右焦点F2(1,0)的直线l与椭圆C交于M,N两点.
=1(a>b>0)上,过椭圆C的右焦点F2(1,0)的直线l与椭圆C交于M,N两点.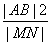 .试判断W是否为定值?若W为定值,请求出这个定值;若W不是定值,请说明理由.
.试判断W是否为定值?若W为定值,请求出这个定值;若W不是定值,请说明理由. 满足条件
满足条件 ,若目标函数
,若目标函数 的最大值为12,则
的最大值为12,则 的最小值为( )
的最小值为( ) B.
B. C.
C. D.4
D.4