题目内容
已知点P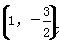 在椭圆C:
在椭圆C: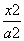 +
+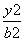 =1(a>b>0)上,过椭圆C的右焦点F2(1,0)的直线l与椭圆C交于M,N两点.
=1(a>b>0)上,过椭圆C的右焦点F2(1,0)的直线l与椭圆C交于M,N两点.
(1)求椭圆C的方程;
(2)若AB是椭圆C经过原点O的弦,且MN∥AB,W=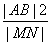 .试判断W是否为定值?若W为定值,请求出这个定值;若W不是定值,请说明理由.
.试判断W是否为定值?若W为定值,请求出这个定值;若W不是定值,请说明理由.
解:(1)椭圆C的右焦点坐标为(1,0),∴c=1,椭圆C的左焦点坐标为(-1,0),
可得2a=
= +
+ =4,
=4,
解得a=2,
∴b2=a2-c2=4-1=3,
∴椭圆C的标准方程为 +
+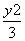 =1.
=1.
(2)①当直线斜率不存在时,|AB|2=(2b)2=4b2,|MN|= ,∴
,∴ =2a=4.
=2a=4.
②当直线斜率存在时,设直线l的方程为y=k(x-1)(k≠0),且M(x1,y1),N(x2,y2).
由 得(3+4k2)x2-8k2x+4k2-12=0,
得(3+4k2)x2-8k2x+4k2-12=0,

 设直线AB的方程为y=kx(k≠0),
设直线AB的方程为y=kx(k≠0),
由 消去y,并整理,得x2=
消去y,并整理,得x2= ,
,
设A(x3,y3),B(x4,y4),
则|AB|= |x3-x4|=4
|x3-x4|=4 ,
,
 综上,W为定值4.
综上,W为定值4.

练习册系列答案
相关题目
 为方程
为方程 的两个实数解,则
的两个实数解,则
 =2
=2 ,则|BC|=( )
,则|BC|=( ) B.6 C.
B.6 C. D.8
D.8
 ,圆C是以坐标原点O为圆心,实轴为直径的圆.过双曲线第一象限内的任一点P(x0,y0)作圆C的两条切线,其切点分别为A,B.若直线AB与x轴、y轴分别相交于M,N两点,则
,圆C是以坐标原点O为圆心,实轴为直径的圆.过双曲线第一象限内的任一点P(x0,y0)作圆C的两条切线,其切点分别为A,B.若直线AB与x轴、y轴分别相交于M,N两点,则 -
- 的值为________.
的值为________.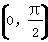 上不是凸函数的是( )
上不是凸函数的是( ) +sin x,其导函数记为f′(x),则f(2 013)+f′(2 013)+f(-2 013)-f′(-2 013)=________.
+sin x,其导函数记为f′(x),则f(2 013)+f′(2 013)+f(-2 013)-f′(-2 013)=________. 中,角
中,角 、
、 、
、 的对边分别是a、b、c。已知
的对边分别是a、b、c。已知 ,则
,则 是 ( )
是 ( )