题目内容
19．已知a，b∈R，则“$\sqrt{a-1}＞\sqrt{b-1}$”是“logab＜1”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
分析 $\sqrt{a-1}＞\sqrt{b-1}$，平方可得a＞b≥1，可得logab＜1，反之不成立，即可得出．
解答 解：$\sqrt{a-1}＞\sqrt{b-1}$，平方可得a＞b≥1，可得logab＜1，
反之不成立，例如取a=$\frac{1}{3}$，b=$\frac{1}{2}$．
∴$\sqrt{a-1}＞\sqrt{b-1}$”是“logab＜1”的充分不必要条件．
故选：A．
点评 本题考查了对数函数的单调性、简易逻辑的判定方法、不等式的解法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
7．运行如图所示的程序框图，则输出的S值为（ ）
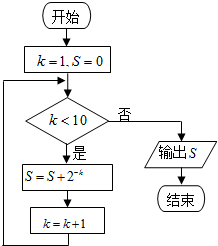
| A． | $\frac{{{2^9}-1}}{2^9}$ | B． | $\frac{{{2^9}+1}}{2^9}$ | C． | $\frac{{{2^{10}}-1}}{{{2^{10}}}}$ | D． | $\frac{{{2^{10}}}}{{{2^{10}}+1}}$ |
14．已知AB为圆x2+y2=1的一条直径，点P为直线x-y+2=0上任意一点，则$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为（ ）
| A． | 1 | B． | $\sqrt{2}$ | C． | 2 | D． | $2\sqrt{2}$ |
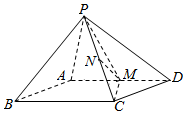如图，四棱锥的底面ABCD是平行四边形，PA⊥平面ABCD，M是AD中点，N是PC中点．