题目内容
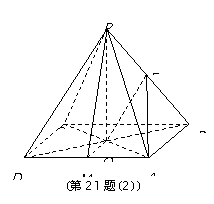
如图所示,正四棱锥P-ABCD中,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为 .
.
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值;
 |
解:(1)取AD中点M,连接MO,PM,依条件可知AD⊥MO,AD⊥PO,
则∠PMO为所求二面角P-AD-O的平面角.∵PO⊥面ABCD,
∴∠PAO为侧棱PA与底面ABCD所成的角.
∴tan∠PAO=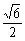 .
.
设AB=a,AO=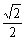 a,∴ PO=AO·tan∠POA=
a,∴ PO=AO·tan∠POA=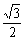 a,
a,
tan∠PMO=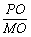 =
=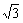 . ∴∠PMO=60°.
. ∴∠PMO=60°.
(2)连接AE,OE, ∵OE∥PD,
∴∠OEA为异面直线PD与AE所成的角.
∵AO⊥BD,AO⊥PO,∴AO⊥平面PBD.又OE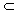 平面PBD,∴AO⊥OE.
平面PBD,∴AO⊥OE.
 ∵OE=
∵OE=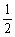 PD=
PD=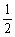
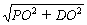 =
=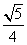 a, ∴tan∠AEO=
a, ∴tan∠AEO=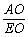 =
=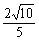 .
.

练习册系列答案
相关题目

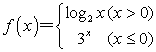 ,则
,则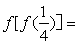 .
. 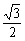 a3,则侧棱与底面所成的角为( ).
a3,则侧棱与底面所成的角为( ).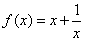 在
在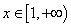 上是增函数。
上是增函数。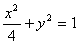 共焦点且过点
共焦点且过点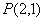 的双曲线方程是( )
的双曲线方程是( ) B
B 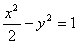 C
C  D
D 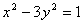
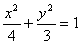 上的点,
上的点,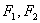 分别是椭圆的左、右焦点,若
分别是椭圆的左、右焦点,若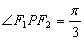 ,则
,则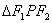 的面积为__________
的面积为__________ 是3a与3b的等比中项,则
是3a与3b的等比中项,则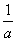 +
+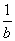 的最小值为________.
的最小值为________.