题目内容
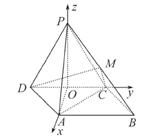
如图,四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是菱形且∠ADC=60°,M为PB的中点.
(1)求PA与底面ABCD所成角的大小.
(2)求证:PA⊥平面CDM.
(3)求二面角D-MC-B的余弦值.

解:(1)取DC的中点O,由△PDC是正三角形,有PO⊥DC.
又∵平面PDC⊥底面ABCD,∴PO⊥平面ABCD于O.
连接OA,则OA是PA在底面上的射影,
∴∠PAO就是PA与底面ABCD所成的角.
∵∠ADC=60°,由已知△PCD和△ACD是全等的正三角形,从而求得OA=OP= .
.
∴∠PAO=45°,∴PA与底面ABCD所成角的大小为45°. ……………4分
(2)由底面ABCD为菱形且∠ADC=60°,DC=2,DO=1,得OA⊥DC.
建立空间直角坐标系如图,
 则A(
则A( ,0,0),P(0,0,
,0,0),P(0,0, ),D(0,-1,0),B(
),D(0,-1,0),B( ,2,0),C(0,1,0).
,2,0),C(0,1,0).
由M为PB中点,∴M(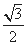 ,1,
,1,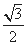 ),
),
∴ =(
=(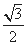 ,2,
,2,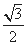 ),
),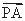 =(
=( ,0,-
,0,- ),
), =(0,2,0),
=(0,2,0),
∴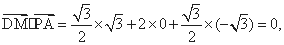
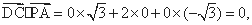
∴PA⊥DM,PA⊥DC.又DM∩DC=D,∴PA⊥平面CDM. ……………8分
(3)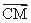 =(
=(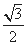 ,0,
,0,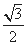 ),
), =(
=( ,1,0).
,1,0).
设平面BMC的法向量n=(x,y,z),
则n·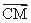 =0,从而x+z=0;①
=0,从而x+z=0;①
n· =0,从而
=0,从而 x+y=0,②
x+y=0,②
由①②,取x=-1,则y= ,z=1.∴可取n=(-1,
,z=1.∴可取n=(-1, ,1).
,1).
由(2)知平面CDM的法向量可取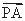 =(
=( ,0,-
,0,- ),
),
∴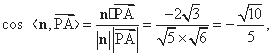
∴所求二面角的余弦值为 . ……………12分
. ……………12分

 有零点的一个区间是 ( )
有零点的一个区间是 ( ) , 499进行编号. 如果从随机数表第8行第4列的数开始三位数连续向右读取, 请你依次写出最先检测的5袋牛奶的编号
, 499进行编号. 如果从随机数表第8行第4列的数开始三位数连续向右读取, 请你依次写出最先检测的5袋牛奶的编号  有相同的焦距,一条渐近线方程为x-2y=0,则双曲线C的标准方程为
有相同的焦距,一条渐近线方程为x-2y=0,则双曲线C的标准方程为 B.
B.
 D.
D.
 为双曲线
为双曲线 的左焦点,
的左焦点, 为
为 上的点,若
上的点,若 的长等于虚轴长的2倍,点
的长等于虚轴长的2倍,点 在线段
在线段 的周长为 .
的周长为 .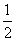 + i B.5 C.
+ i B.5 C.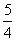 D.
D.
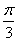 ) 的值是
) 的值是 ,
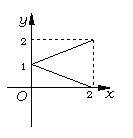
,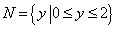 ,给出如下四个图形,其中能表示从集合
,给出如下四个图形,其中能表示从集合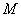 到集合
到集合 的函数关系的是( )
的函数关系的是( )


 .
.