题目内容
1.已知数列{an},其前n项和为Sn.(1)若{an}是公差为d(d>0)的等差数列,且{$\sqrt{{S}_{n}+n}$}也为公差为d的等差数列,求数列{an}的通项公式;
(2)若数列{an}对任意m,n∈N*,且m≠n,都有$\frac{2{S}_{m+n}}{m+n}$=am+an+$\frac{{a}_{m}-{a}_{n}}{m-n}$,求证:数列{an}是等差数列.
分析 (1)利用等差数列的通项公式及前n项和公式表示出an与Sn,代入验证即可确定出数列{an}的通项公式;
(2)令m=2,n=1确定出a1,a2,a3成等差数列,再利用数学归纳法证明对于一切n≥3的自然数,数列{an}是等差数列即可.
解答 解:(1)根据题意得:an=a1+(n-1)d,Sn=na1+$\frac{n(n-1)}{2}$d,
∴$\sqrt{{S}_{n}+n}$=$\sqrt{n({a}_{1}+\frac{n-1}{2}d+1)}$成等差数列,公差为d,
∴$\sqrt{{S}_{n}+n}$=dn,
∴$\left\{\begin{array}{l}{{a}_{1}+1-\frac{d}{2}=0}\\{\sqrt{\frac{d}{2}}=d}\end{array}\right.$,
解得:d=$\frac{1}{2}$,a1=-$\frac{3}{4}$,
则an=$\frac{1}{2}$n-$\frac{5}{4}$;
(2)令m=2,n=1,则$\frac{2{S}_{3}}{3}$=2a2,即$\frac{{a}_{1}+{a}_{2}+{a}_{3}}{3}$=a2,
整理得:a1+a3=2a2,即a1,a2,a3成等差数列,
下面用数学归纳法证明{an}成等差数列,
假设a1,a2,…,ak成等差数列,其中k≥3,公差为d,
则令m=k,n=1,$\frac{2{S}_{k+1}}{k+1}$=ak+a1+d,
∴2Sk+1=(k+1)(ak+a1+d)=k(ak+a1)+a1+ak+(k+1)d=2Sk+a1+ak+(k+1)d,
∴2ak+1=a1+ak+(k+1)d=2(a1+kd),即ak+1=a1+kd,
∴a1,a2,…,ak,ak+1成等差数列,
则对于一切自然数,数列{an}是等差数列.
点评 此题考查了等差数列的性质,以及等差关系的确定,熟练掌握等差数列的性质是解本题的关键.

| A. | (0,+∞) | B. | (1,+∞) | C. | (e,+∞) | D. | $(\frac{e}{3},+∞)$ |
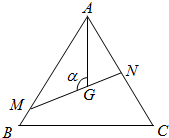 如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.
如图,是△ABC边长为1的正三角形,M,N分别是AB,AC边上的点,线段MN过△ABC的重心,设∠MGA=α,$\frac{π}{3}$≤α≤$\frac{2π}{3}$.