题目内容
17．已知曲线x2-4y2=4，过点A（3，-1）且被点A平分的弦MN所在的直线方程为3x+4y-5=0．分析 设两个交点的坐标分别为（x1，y1），（x2，y2），利用点差法求得直线的斜率，进一步求出直线方程，然后验证直线与曲线方程由两个交点即可．
解答 解：设两个交点的坐标分别为（x1，y1），（x2，y2）
所以x12-4y12=4，x22-4y12=4，两式相减得（x1+x2）（x1-x2）=4（y1+y2）（y1-y2），
又$\frac{{x}_{1}+{x}_{2}}{2}$=3，$\frac{{y}_{1}+{y}_{2}}{2}$=-1，∴$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{3}{4}$，
所以直线的方程为y+1=-$\frac{3}{4}$（x-3），即3x+4y-5=0．
由点A（3，-1）在双曲线内部，直线方程满足题意．
∴MN所在直线的方程是3x+4y-5=0．
故答案为：3x+4y-5=0．
点评 本题主要考查了直线与圆锥曲线的综合问题．解题的关键是充分运用数形结合的数学思想、方程的数学思想和转化的数学思想来解决较为复杂的综合题．
练习册系列答案
阅读快车系列答案
相关题目
7．下列函数中是偶函数的是（ ）
| A． | f（x）=x2+1，x∈[-2，2） | B． | f（x）=|3x-1|-|3x+1| | ||
| C． | f（x）=-x2+1，x∈（-2，+∞） | D． | f（x）=x4 |
8．
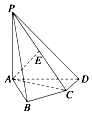如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．
（1）证明：AE⊥平面PCD；
（2）求PB和平面PAD所成的角的大小．
如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．（1）证明：AE⊥平面PCD；
（2）求PB和平面PAD所成的角的大小．
2．已知函数f（x）=sin|ωx|，若y=f（x）与y=m（m=-1）图象的公共点中，相邻两个公共点的距离的最大值为2π，则ω的值为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\frac{3}{2}$ | D． | 2 |
6．已知命题p：?x0∈[1，2]，x02-4x0+6＜0，则￢p为（ ）
| A． | ?x∉[1，2]，x2-4x+6≥0 | B． | ?x0∈[1，2]，x02-4x0+6≥0 | ||
| C． | ?x∉[1，2]，x2-4x+6＞0 | D． | ?x∈[1，2]，x2-4x+6≥0 |
7．数列{an}的通项公式为${a_n}={n^2}+kn$，那么k≥-2是{an}为递增数列的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |