题目内容
2.已知函数f(x)=sin|ωx|,若y=f(x)与y=m(m=-1)图象的公共点中,相邻两个公共点的距离的最大值为2π,则ω的值为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
分析 根据f(x)的图象特征以及f(x)的图象与y=-1相邻两个公共点的距离的最大值为$\frac{3}{2}$•T=$\frac{3}{2}$•$\frac{2π}{ω}$=2π,求得ω的值.
解答 解:函数f(x)=sin|ωx|,若y=f(x)与y=m(m=-1)图象的公共点中,
相邻两个公共点的距离的最大值为$\frac{3}{2}$•T=$\frac{3}{2}$•$\frac{2π}{ω}$=2π,则ω=$\frac{3}{2}$,
故选:C.
点评 本题主要考查正弦函数的图象,y=sin|ωx|的图象特征,属于基础题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
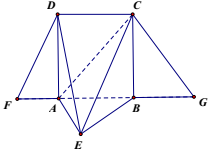 如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.
如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上. 如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.
如图,已知△ABC中,D为边BC上靠近B点的三等分点,连接AD,E为线段AD的中点,若$\overrightarrow{CE}=m\overrightarrow{AB}+n\overrightarrow{AC}$,则m+n=$-\frac{1}{2}$.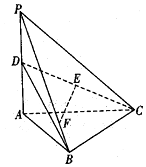 如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.
如图,三棱锥P-ABC中,PA⊥平面ABC,∠ABC=90°,PA=AC=2,D是PA的中点,E是CD的中点,点F在PB上,$\overrightarrow{PF}=3\overrightarrow{FB}$.