题目内容
5.已知命题p:|x+2|>1,命题q:x<a,且p是q的必要不充分条件,则a的取值范围是(-∞,-3].分析 根据充分必要条件的定义求出a的范围即可.
解答 解:由|x+2|>1,解得:x>-1或x<-3,
故命题p:{x|x>-1或x<-3},
命题q:x<a,
若p是q的必要不充分条件,
故a≤-3,
故答案为:(-∞,-3].
点评 本题考查了充分必要条件的定义,考查集合的包含关系,是一道基础题.

练习册系列答案
相关题目
15.已知$a={(\frac{1}{3})}^{-3},b={(0.3)}^{2},c={log}_{\frac{1}{2}}3$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>b>a |
16.设P,Q分别为椭圆$\frac{x^2}{10}+{y^2}=1$和圆x2+(y-6)2=2上的点,则P,Q两点间的最大距离是( )
| A. | $7+\sqrt{2}$ | B. | $6\sqrt{2}$ | C. | $5\sqrt{2}$ | D. | $\sqrt{46}+\sqrt{2}$ |
14.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(1,x),若$\overrightarrow{a}$+$\overrightarrow{b}$与$2\overrightarrow a-\overrightarrow b$平行,则实数x的值是( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
15.已知A+B=$\frac{π}{3}$,则tanA+tanB+$\sqrt{3}$tanAtanB-$\sqrt{3}$的值等于( )
| A. | -2$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 0 | D. | 1-$\sqrt{3}$ |
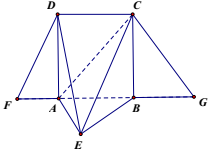 如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.
如图,梯形FDCG,DC∥FG,过点D,C作DA⊥FG,CB⊥FG,垂足分别为A,B,且DA=AB=2.现将△DAF沿DA,△CBG沿CB翻折,使得点F,G重合,记为E,且点B在面AEC的射影在线段EC上.