题目内容
7.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,过点F作x轴的垂线与双曲线交于B,C两点(点B在x轴上方),过点B作斜率为负数的渐近线的垂线,过点C作斜率为正数的渐近线的垂线,两垂线交于点D,若D到直线BC的距离小于虚轴长的2倍,则双曲线的离心率e的取值范围是( )| A. | 1<e<$\sqrt{3}$ | B. | e>$\sqrt{3}$ | C. | 1<e<$\sqrt{5}$ | D. | e>$\sqrt{5}$ |
分析 求出直线BD的方程,可得D的坐标,利用D到直线BC的距离小于虚轴长的2倍,可得不等式,即可求出双曲线的离心率e的取值范围.
解答 解:由题意,B(c,$\frac{{b}^{2}}{a}$),直线BD的方程为y-$\frac{{b}^{2}}{a}$=$\frac{a}{b}$(x-c),
令y=0,可得x=c-$\frac{{b}^{3}}{{a}^{2}}$,根据对称性,可得D(c-$\frac{{b}^{3}}{{a}^{2}}$,0),
∵D到直线BC的距离小于虚轴长的2倍,
∴$\frac{{b}^{3}}{{a}^{2}}$<4b,∴c2-a2<4a2,
∵e>1,∴1<e<$\sqrt{5}$,
故选C.
点评 本题考查双曲线的离心率e的取值范围,考查直线方程,考查学生的计算能力,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
17.已知函数$f(x)=\frac{2x}{x-1}≥a$在区间[3,5]上恒成立,则实数a的最大值是( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
15.已知y=f(x)是定义在R上的奇函数,当x>0时,f(x)=x-2,那么不等式$f(x)<\frac{1}{2}$的解集是( )
| A. | $\left\{{x|0<x<\frac{5}{2}}\right\}$ | B. | $\left\{{x|x<-\frac{3}{2}\;,\;\;或0≤x<\frac{5}{2}}\right\}$ | ||
| C. | $\left\{{x|-\frac{3}{2}<x<0\;,\;\;或0≤x<\frac{5}{2}}\right\}$ | D. | $\left\{{x|-\frac{3}{2}<x<0}\right\}$ |
12.已知集合M=(0,+∞),N=[0,+∞),那么下列关系成立的是( )
| A. | M?N | B. | N?M | C. | M⊆N | D. | M∩N=∅ |
16.设a为实数,直线l1:ax+y=1,l2:x+ay=2a,则“a=-1”是“l1∥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也必要条件 |
17.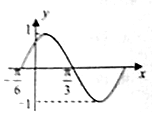 函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1+x2=$\frac{2π}{3}$,则f(x1)+f(x2)=( )
函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1+x2=$\frac{2π}{3}$,则f(x1)+f(x2)=( )
 函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1+x2=$\frac{2π}{3}$,则f(x1)+f(x2)=( )
函数f(x)=sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,如果x1+x2=$\frac{2π}{3}$,则f(x1)+f(x2)=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |