题目内容
12．已知集合M=（0，+∞），N=[0，+∞），那么下列关系成立的是（ ）| A． | M?N | B． | N?M | C． | M⊆N | D． | M∩N=∅ |
分析 由题意，M中元素都是N中元素，N中0不是M中元素，即可得出结论．
解答 解：由题意，M中元素都是N中元素，N中0不是M中元素，则M?N，
故选A．
点评 本题考查集合的包含关系，考查学生分析解决问题的能力，比较基础．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
3．若sinα=3cosα，则$\frac{sin2α}{{{{cos}^2}α}}$=（ ）
| A． | 2 | B． | 3 | C． | 4 | D． | 6 |
20．
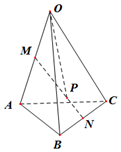已知M、N分别是四面体OABC的棱OA，BC的中点，点P在线MN上，且MP=2PN，设向量$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则$\overrightarrow{OP}$=（ ）
已知M、N分别是四面体OABC的棱OA，BC的中点，点P在线MN上，且MP=2PN，设向量$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则$\overrightarrow{OP}$=（ ）| A． | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ | B． | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C． | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D． | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ |
7．设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点为F，过点F作x轴的垂线与双曲线交于B，C两点（点B在x轴上方），过点B作斜率为负数的渐近线的垂线，过点C作斜率为正数的渐近线的垂线，两垂线交于点D，若D到直线BC的距离小于虚轴长的2倍，则双曲线的离心率e的取值范围是（ ）
| A． | 1＜e＜$\sqrt{3}$ | B． | e＞$\sqrt{3}$ | C． | 1＜e＜$\sqrt{5}$ | D． | e＞$\sqrt{5}$ |
17．函数y=f（x）满足对任意x∈R都有f（x+2）=f（-x）成立，且函数y=f（x-1）的图象关于点（1，0）对称，f（1）=4，则f（2016）+f（2017）+f（2018）=（ ）
| A． | 12 | B． | 8 | C． | 4 | D． | 0 |
4．已知函数f（x）=sin（2x+$\frac{π}{6}$）+cos2x，则f（x）的一个单调递减区间是（ ）
| A． | [$\frac{π}{12}$，$\frac{7π}{12}$] | B． | [-$\frac{5π}{12}$，$\frac{π}{12}$] | C． | [-$\frac{π}{3}$，$\frac{2π}{3}$] | D． | [-$\frac{π}{6}$，$\frac{5π}{6}$] |