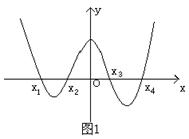
题目内容
求函数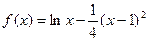 在[1,3]上的最大值和最小值.
在[1,3]上的最大值和最小值.
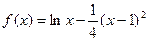 在[1,3]上的最大值和最小值.
在[1,3]上的最大值和最小值.f(1)=0是函数f(x)在[1,3]上的最小值,
f(2)=ln2- 为f(x)在[1,3]的最大值
为f(x)在[1,3]的最大值
f(2)=ln2-
 为f(x)在[1,3]的最大值
为f(x)在[1,3]的最大值 ……………………………………………………(2分)
……………………………………………………(2分)由

化简得x2-x-2="0 " 解得x1=-1(舍)或x2=2………………………………(4分)
当x∈(1,2)时,
 >0,f(x)在x∈(1,2)上单调递增,
>0,f(x)在x∈(1,2)上单调递增,当x∈(2,3)时,
 <0,f(x)在x∈(2,3)上单调递减…………(6分)
<0,f(x)在x∈(2,3)上单调递减…………(6分)又f(x)在[1,3]上连续,所以f(2)=ln2-
 为函数f(x)的极大值…………(8分)
为函数f(x)的极大值…………(8分)又∵f(1)=0,f(3)=ln3-1>0
∴f(3)>f(1)所以f(1)=0是函数f(x)在[1,3]上的最小值,
f(2)=ln2-
 为f(x)在[1,3]的最大值…………………………………………(12分)
为f(x)在[1,3]的最大值…………………………………………(12分)
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
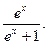
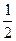 )对称;
)对称;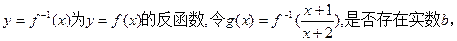 使得任给
使得任给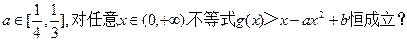 若存在,求b的取值范围;若不存在,说明理由.
若存在,求b的取值范围;若不存在,说明理由.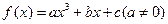 ,
,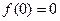 ,其图象在点
,其图象在点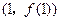 处的切线与直线
处的切线与直线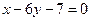 垂直,导函数
垂直,导函数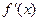 的最小值为
的最小值为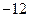 .
.
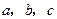 的值;
的值;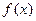 的单调递增区间,并求函数
的单调递增区间,并求函数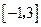 上的最大值和最小值.
上的最大值和最小值.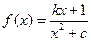 (
(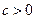 且
且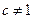 ,
,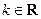 )恰有一个极大值点和一个极小值点,其中一个是
)恰有一个极大值点和一个极小值点,其中一个是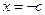 .
.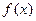 的另一个极值点;
的另一个极值点;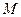 和极小值
和极小值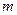 ,并求
,并求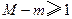 时
时 的取值范围.
的取值范围.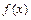 的二次项系数为
的二次项系数为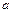 ,且不等式
,且不等式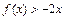 的解集为
的解集为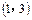

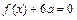 有两个相等的实数根,求
有两个相等的实数根,求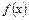 的解析式;
的解析式;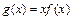 无极值,求实数
无极值,求实数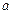 的取值范围
的取值范围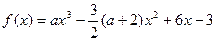
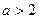 时,求函数
时,求函数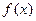 的极小值
的极小值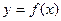 与
与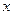 轴的公共点的个数。
轴的公共点的个数。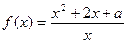
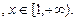 当
当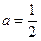 时,求函数
时,求函数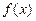 的最小值;
的最小值;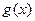 中
中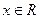 ,其导
,其导 函数
函数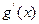 的图象如图1,则函数
的图象如图1,则函数