题目内容
13.已知(1+2x)n的展开式中各项的二项式系数和为an,第二项的系数为bn.(1)求an,bn;
(2)求数列{anbn}的前n项和Sn.
分析 (1)由二项式系数的性质和二项展开式的通项公式,可得an,bn;
(2)求得anbn=n•2n+1,运用数列的求和方法:错位相减法,结合等比数列的求和公式,即可得到所求和.
解答 解:(1)(1+2x)n的展开式中各项的二项式系数和为an,第二项的系数为bn.
可得an=2n,bn=2${C}_{n}^{1}$=2n;
(2)anbn=n•2n+1,
则前n项和Sn=1•22+2•23+…+n•2n+1,
2Sn=1•23+2•24+…+n•2n+2,
两式相减可得,-Sn=22+23+…+2n+1-n•2n+2,
=$\frac{4(1-{2}^{n})}{1-2}$-n•2n+2,
化简可得Sn=(n-1)•2n+2+4.
点评 本题考查二项式系数的性质和二项展开式的通项公式,同时考查数列的求和方法:错位相减法,同时考查等比数列的求和公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
1.sin72°cos18°+cos72°sin18°的值为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
3.以下关于正弦定理或其变形的叙述错误的是( )
| A. | 在△ABC中,a:b:c=sinA:sinB:sinC | |
| B. | 在△ABC中,若sin2A=sin2B,则a=b | |
| C. | 在△ABC中,若sinA>sinB,则A>B,若A>B,则sinA>sinB | |
| D. | 在△ABC中,$\frac{a}{sinA}=\frac{b+c}{sinB+sinC}$ |
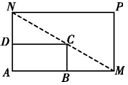 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B点在AM上,D点在AN上,且对角线MN过点C,已知AB=2米,AD=1米.