题目内容
设数列{an}是各项均为正数的等比数列,其前n项和为Sn,若a1a5=64,S5-S3=48.
(1)求数列{an}的通项公式;
(2)对于正整数k,m,l(k<m<l),求证:“m=k+1且l=k+3”是“5ak,am,al这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列{bn}满足:对任意的正整数n,都有a1bn+a2bn-1+a3bn-2+…+anb1=3•2n+1-4n-6,且集合M={n|
≥λ,n∈N*}中有且仅有3个元素,试求λ的取值范围.
(1)求数列{an}的通项公式;
(2)对于正整数k,m,l(k<m<l),求证:“m=k+1且l=k+3”是“5ak,am,al这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列{bn}满足:对任意的正整数n,都有a1bn+a2bn-1+a3bn-2+…+anb1=3•2n+1-4n-6,且集合M={n|
| bn |
| an |
考点:等差数列与等比数列的综合,数列与不等式的综合
专题:等差数列与等比数列
分析:(1)由题意和等比数列的性质先求出a3,由等比数列的通项公式、前n项和的定义求出公比q,代入等比数列的通项公式化简即可;
(2)由充要条件的定义分别证明充分性、必要性,顺序分类讨论后分别利用等差数列的性质和an进行证明;
(3)由(1)化简a1bn+a2bn-1+a3bn-2+…+anb1=3•2n+1-4n-6后,两边同乘以2再作差求出bn,注意验证n=1是否成立代入
,利用作差判断数列{
}的单调性,再求出符合条件的λ的范围.
(2)由充要条件的定义分别证明充分性、必要性,顺序分类讨论后分别利用等差数列的性质和an进行证明;
(3)由(1)化简a1bn+a2bn-1+a3bn-2+…+anb1=3•2n+1-4n-6后,两边同乘以2再作差求出bn,注意验证n=1是否成立代入
| bn |
| an |
| bn |
| an |
解答:
解:(1)设等比数列{an}的公比是q,
∵数列{an}是各项均为正数的等比数列,∴a1a5=a32=64,解得a3=8,
又∵S5-S3=48,∴a4+a5=8q2+8q=48,解得q=2,
∴an=8•2n-3=2n; …4分
(2)(ⅰ)必要性:设5ak,am,al这三项经适当排序后能构成等差数列,
①若2•5ak=am+al,则10•2k=2m+2l,∴10=2m-k+2l-k,∴5=2m-k-1+2l-k-1,
∴
,∴
.…6分
②若2am=5ak+al,则2•2m=5•2k+2l,∴2m+1-k-2l-k=5,左边为偶数,等式不成立,
③若2al=5ak+am,同理也不成立,
综合①②③,得m=k+1,l=k+3,所以必要性成立.…8分
(ⅱ)充分性:设m=k+1,l=k+3,
则5ak,am,al这三项为5ak,ak+1,ak+3,即5ak,2ak,8ak,
调整顺序后易知2ak,5ak,8ak成等差数列,
所以充分性也成立.
综合(ⅰ)(ⅱ),原命题成立.…10分
(3)因为a1bn+a2bn-1+a3bn-2+…+anb1=3•2n+1-4n-6,
即21bn+22bn-1+23bn-2+…+2nb1=3•2n+1-4n-6,①
∴当n≥2时,21bn-1+22bn-2+23bn-3+…+2n-1b1=3•2n-4n-2,②
则②式两边同乘以2,得22bn-1+23bn-2+24bn-3+…+2nb1=3•2n+1-8n-4,③
∴①-③,得2bn=4n-2,即bn=2n-1(n≥2),
又当n=1时,2b1=3•22-10=2,即b1=1,适合bn=2n-1(n≥2),
∴bn=2n-1.…14分
∴
=
,∴
-
=
-
=
,
∴n=2时,
-
>0,即
>
;
∴n≥3时,
-
<0,此时{
}单调递减,
又
=
,
=
,
=
,
=
,∴
<λ≤
.…16分
∵数列{an}是各项均为正数的等比数列,∴a1a5=a32=64,解得a3=8,
又∵S5-S3=48,∴a4+a5=8q2+8q=48,解得q=2,
∴an=8•2n-3=2n; …4分
(2)(ⅰ)必要性:设5ak,am,al这三项经适当排序后能构成等差数列,
①若2•5ak=am+al,则10•2k=2m+2l,∴10=2m-k+2l-k,∴5=2m-k-1+2l-k-1,
∴
|
|
②若2am=5ak+al,则2•2m=5•2k+2l,∴2m+1-k-2l-k=5,左边为偶数,等式不成立,
③若2al=5ak+am,同理也不成立,
综合①②③,得m=k+1,l=k+3,所以必要性成立.…8分
(ⅱ)充分性:设m=k+1,l=k+3,
则5ak,am,al这三项为5ak,ak+1,ak+3,即5ak,2ak,8ak,
调整顺序后易知2ak,5ak,8ak成等差数列,
所以充分性也成立.
综合(ⅰ)(ⅱ),原命题成立.…10分
(3)因为a1bn+a2bn-1+a3bn-2+…+anb1=3•2n+1-4n-6,
即21bn+22bn-1+23bn-2+…+2nb1=3•2n+1-4n-6,①
∴当n≥2时,21bn-1+22bn-2+23bn-3+…+2n-1b1=3•2n-4n-2,②
则②式两边同乘以2,得22bn-1+23bn-2+24bn-3+…+2nb1=3•2n+1-8n-4,③
∴①-③,得2bn=4n-2,即bn=2n-1(n≥2),
又当n=1时,2b1=3•22-10=2,即b1=1,适合bn=2n-1(n≥2),
∴bn=2n-1.…14分
∴
| bn |
| an |
| 2n-1 |
| 2n |
| bn |
| an |
| bn-1 |
| an-1 |
| 2n-1 |
| 2n |
| 2n-3 |
| 2n-1 |
| 5-2n |
| 2n |
∴n=2时,
| bn |
| an |
| bn-1 |
| an-1 |
| b2 |
| a2 |
| b1 |
| a1 |
∴n≥3时,
| bn |
| an |
| bn-1 |
| an-1 |
| bn |
| an |
又
| b1 |
| a1 |
| 1 |
| 2 |
| b2 |
| a2 |
| 3 |
| 4 |
| b3 |
| a3 |
| 5 |
| 8 |
| b4 |
| a4 |
| 7 |
| 16 |
| 7 |
| 16 |
| 1 |
| 2 |
点评:本题考查等差数列、等比数列的性质,作差法判断数列的单调性,考查分类讨论思想的运用,计算化简、变形能力与逻辑推理能力,属于难题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
复数z=
的共轭复数是( )
| -3+i |
| 2+i |
| A、-1-i | B、2-i |
| C、-1+i | D、2+i |
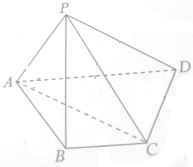 如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.
如图四棱锥P-ABCD的底面是梯形,BC∥AD,AB=BC=CD=1,AD=2,平面PAC⊥平面ABCD.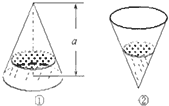 如图①,一个圆锥形容器的高为a=2,内装有高度为h的一定量的水,如果将容器倒置,这时水所形成的圆锥的高恰为1(如图②),则图①中的水面高度h=
如图①,一个圆锥形容器的高为a=2,内装有高度为h的一定量的水,如果将容器倒置,这时水所形成的圆锥的高恰为1(如图②),则图①中的水面高度h=