题目内容
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系的x轴的正半轴重合．设点O为坐标原点，直线l：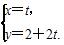
(参数t∈R)与曲线C的极坐标方程为ρcos2θ＝2sinθ.
(1)求直线l与曲线C的普通方程；
(2)设直线l与曲线C相交于A、B两点，证明：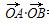
＝0.
[解析] (1)由直线的参数方程消去参数t得普通方程y＝2x＋2；由曲线C的极坐标方程得曲线C的普通方程为x2＝2y，
(2)设A(x1，y1)，B(x2，y2)，由
消去y得x2－4x－4＝0，
x1＋x2＝4，x1·x2＝－4，∴y1y2＝
·
＝4，
练习册系列答案
相关题目
.
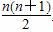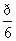)，则过点P且平行于极轴的直线的方程是( )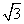
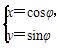(φ为参数)，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，圆C2的极坐标方程为ρ＝2cos(θ＋
)．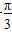