题目内容
用数学归纳法证明下面的等式12－22＋32－42＋…＋(－1)n－1·n2＝(－1)n－1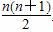
.
(1)当n＝1时，左边＝12＝1，
右边＝(－1)0·
＝1，
∴原等式成立．
(2)假设n＝k(k∈N＋，k≥1)时，等式成立，
即有12－22＋32－42＋…＋(－1)k－1·k2
＝(－1)k－1
.
那么，当n＝k＋1时，则有
12－22＋32－42＋…＋(－1)k－1·k2＋(－1)k·(k＋1)2
∴n＝k＋1时，等式也成立，
由(1)(2)得对任意n∈N＋有
12－22＋32－42＋…＋(－1)n－1·n2
＝
.
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
(i为虚数单位)在复平面内对应的点所在的象限为( )
≤an－an＋1成立．
的大小，并证明你的结论．
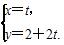(参数t∈R)与曲线C的极坐标方程为ρcos2θ＝2sinθ.
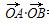＝0.