题目内容
2.已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,则a-b=( )| A. | -7 | B. | -2 | C. | -7和-2 | D. | 以上答案都不对 |
分析 求导函数,利用函数f(x)=x3+3ax2+bx+a2在x=-1处有极值0,建立方程组,求得a,b的值,再验证,即可得到结论.
解答 解:∵函数f(x)=x3+3ax2+bx+a2,
∴f'(x)=3x2+6ax+b,
又∵函数f(x)=x3+3ax2+bx+a2在x=-1处有极值0,
∴$\left\{\begin{array}{l}{3-6a+b=0}\\{-1+3a-b+{a}^{2}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=2}\\{b=9}\end{array}\right.$,
当$\left\{\begin{array}{l}{a=1}\\{b=3}\end{array}\right.$时,f'(x)=3x2+6ax+b=3(x+1)2=0,方程有两个相等的实数根,不满足题意;
当$\left\{\begin{array}{l}{a=2}\\{b=9}\end{array}\right.$时,f'(x)=3x2+6ax+b=3(x+1)(x+3)=0,方程有两个不等的实数根,满足题意;
∴a-b=-7
故选:A.
点评 本题考查导数知识的运用,考查函数的极值,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
7.下列各角中与110°角的终边相同的角是( )
| A. | -260° | B. | 470° | C. | 840° | D. | -600° |
12.已知 an=$\frac{n-1}{n+1}$,那么数列{an}是( )
| A. | 递减数列 | B. | 递增数列 | C. | 常数列 | D. | 摆动数列 |
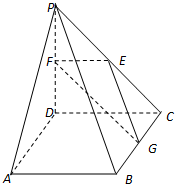 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.